题目内容
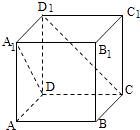
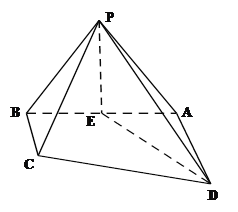
【题目】如图,四棱锥P—ABCD中,底面ABCD是直角梯形,∠DAB=90°,AD//BC,且BC⊥PB,△PAB是等边三角形,DA=AB=2,BC=![]() AD,E是线段AB的中点.
AD,E是线段AB的中点.
(I)求证:PE⊥CD;
(II)求PC与平面PDE所成角的正弦值.
【答案】(1)见解析(2)PC与平面PDE所成角的正弦值为![]()
【解析】【试题分析】(1)先证明线面垂直,再运用线面垂直的性质定理分析推证;(2)建立空间向量,运用向量的坐标形式及向量的数量积公式分析求解:
解:(I)证明:因为BC⊥AB,BC⊥PB,
所以BC⊥侧面PAB,
PE![]() 平面PAB,所以BC⊥PE.
平面PAB,所以BC⊥PE.
又因为△PAB是等边三角形,E是线段AB的中点,
所以PE⊥AB.
因为AD∩AB=A,
所以PE⊥平面ABCD.
而CD![]() 平面ABCD,所以PE⊥CD.
平面ABCD,所以PE⊥CD.
(II)以E为原点,建立如图所示的空间直角坐标系E—xyz.
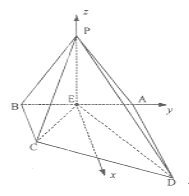
则E(0,0,0),C(1,-1,0),D(2,1,0),P(0,0, ![]() )
)
有![]() ,
,![]() ,
,![]()
设![]() =(x,y,z)为平面PDE的法向量.
=(x,y,z)为平面PDE的法向量.
由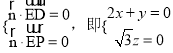
令x=1可得![]()
设PC与平面PDE所成的角为![]()
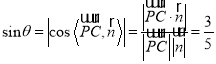
所以PC与平面PDE所成角的正弦值为![]()

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目