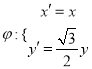题目内容
【题目】如图,已知直线![]() 关于直线
关于直线![]() 对称的直线为
对称的直线为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 分别交于点
分别交于点![]() 、
、![]() 和
和![]() 、
、![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)当![]() 变化时,试问直线
变化时,试问直线![]() 是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点? 若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.

【答案】(Ⅰ)1;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)可以设直线![]() 的方程为
的方程为![]() ,再设直线
,再设直线![]() 上任意一点
上任意一点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() ,于是分别表示出
,于是分别表示出![]() ,由直线对称性可知,
,由直线对称性可知, ![]() 所在直线与
所在直线与![]() 垂直,且
垂直,且![]() 中点在
中点在![]() 上,于是整理得出
上,于是整理得出![]() 的值;(Ⅱ)本问考查椭圆中直线过定点问题,设
的值;(Ⅱ)本问考查椭圆中直线过定点问题,设![]() ,将AM方程与椭圆方程联立,可以求出点M的坐标,同理将直线AN方程与椭圆方程联立,可以求出点N的坐标,根据M,N两点坐标,可以求出直线MN的方程,从而判定直线MN是否过定点.
,将AM方程与椭圆方程联立,可以求出点M的坐标,同理将直线AN方程与椭圆方程联立,可以求出点N的坐标,根据M,N两点坐标,可以求出直线MN的方程,从而判定直线MN是否过定点.
试题解析:(Ⅰ)设直线![]() 上任意一点
上任意一点![]() 关于直线
关于直线![]() 对称点为
对称点为![]()

直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,∴
,∴![]()
![]() ,由
,由![]()
得![]() ……..①
……..①
由![]() 得
得![]() …….②,
…….②,
由①②得 ![]()
![]() .
.
(Ⅱ)设点![]() ,由
,由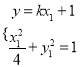 得
得![]() ,
,
∴![]() ,∴
,∴![]() .
.
同理: ![]() ,
, ![]()
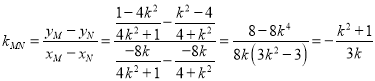
![]() ,∴
,∴![]()
即: 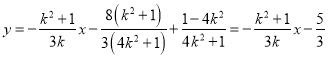
∴当![]() 变化时,直线
变化时,直线![]() 过定点
过定点![]() .
.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取![]() 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
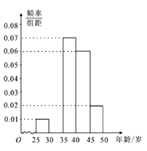
(1)求频率分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取![]() 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这![]() 名市民中年龄在
名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.