题目内容
7.函数f(x)是周期为4的偶函数,当x∈[0,2]时,f(x)=x-1,则不等式xf(x)>0在[-1,3]上的解集为( )
| A. | (1,3) | B. | (-1,1) | C. | (-1,0)∪(1,3) | D. | (-1,0)∪(0,1) |
分析 根据函数的周期性和奇偶性,求出当x∈[-1,3]上的解析式,结合图象将不等式转化为$\left\{\begin{array}{l}{x>0}\\{f(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)<0}\end{array}\right.$,利用数形结合即可得到结论.
解答 解:若x∈[-2,0],则-x∈[0,2],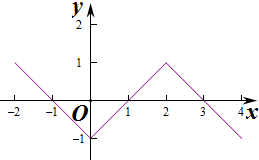
∵当x∈[0,2]时,f(x)=x-1,
∴f(-x)=-x-1,
∵f(x)是偶函数,
∴f(-x)=-x-1=f(x),
即当x∈[-2,0]时,f(x)=-x-1,
即在一个周期[-2,2]内,f(x)=$\left\{\begin{array}{l}{x-1,}&{0≤x≤2}\\{-x-1,}&{-2≤x<0}\end{array}\right.$,
若x∈[2,4],则x-4∈[-2,0],
即f(x)=f(x-4)=-(x-4)-1=-x+3,x∈[2,4],
作出函数f(x)在[-2,4]上的图象如图:
则当x∈[-1,3]时,不等式xf(x)>0
等价为$\left\{\begin{array}{l}{x>0}\\{f(x)>0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)<0}\end{array}\right.$,
即1<x<3或-1<x<0,
即(-1,0)∪(1,3),
故选:C
点评 本题主要考查不等式的解集的计算,根据函数的奇偶性和周期性求出函数的解析式,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
20.若a=20.5,b=logπ3,c=log2sin$\frac{5π}{2}$,则( )
| A. | b>c>a | B. | b>a>c | C. | a>b>c | D. | c>a>b |
20.已知曲线y=x+lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=( )
| A. | -2 | B. | 0 | C. | 1 | D. | 8 |
17.2005年某市的空气质量状况分布如表:
其中X≤50时,空气质量为优,50≤X≤100时空气质量为良,100≤X≤150时,空气质量为轻微污染.
(1)求E(X)的值;
(2)求空气质量达到优或良的概率.
| 污染指数X | 30 | 60 | 100 | 110 | 130 | 140 |
| P | $\frac{1}{10}$ | $\frac{1}{6}$ | $\frac{1}{3}$ | $\frac{7}{30}$ | $\frac{2}{15}$ | $\frac{1}{30}$ |
(1)求E(X)的值;
(2)求空气质量达到优或良的概率.
2.已知△ABC是腰长为2等腰直角三角形,D点是斜边AB的中点,点P在CD上,且$\overrightarrow{CP}=\frac{1}{2}\overrightarrow{PD}$,则$\overrightarrow{PA}•\overrightarrow{PB}$=( )
| A. | -$\frac{3}{4}$ | B. | -$\frac{10}{9}$ | C. | 0 | D. | 4 |
15.设a,b为正数,且a<b,记$P=\frac{a}{b}$,$Q=\frac{a+m}{b+m}$(m>0),则( )
| A. | P=Q | B. | P>Q | ||
| C. | P<Q | D. | P,Q大小关系不确定 |
14.若向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-3,1),则2$\overrightarrow{a}$-$\overrightarrow{b}$=( )
| A. | (5,3) | B. | (5,1) | C. | (-1,3) | D. | (-5,-3) |