题目内容
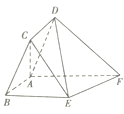
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,侧棱
为矩形,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(Ⅰ)求直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(Ⅱ)在侧面![]() 内找一点
内找一点![]() ,使
,使![]() 面
面![]() ,求N点的坐标。
,求N点的坐标。
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)设AC∩BD=O,连OE,将PB平移到OE,根据异面直线所成角的定义可知∠EOA即为AC与PB所成的角或其补角,在△AOE中,利用余弦定理求出此角的余弦值即可;(Ⅱ)在面ABCD内过D作AC的垂线交AB于F,连PF,设N为PF的中点,连NE,则NE∥DF,根据线面垂直的判定定理可知DF⊥面PAC,从而NE⊥面PAC
试题解析:(Ⅰ)建立如图所示的空间直角坐标系,则![]() 的坐标为
的坐标为![]() 、
、
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
从而![]()
设![]() 的夹角为
的夹角为![]() ,则
,则
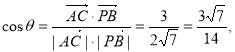
∴![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
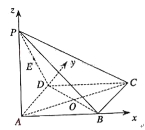
(Ⅱ)由于![]() 点在侧面
点在侧面![]() 内,故可设
内,故可设![]() 点坐标为
点坐标为![]() ,则
,则
![]() ,由
,由![]() 面
面![]() 可得,
可得,
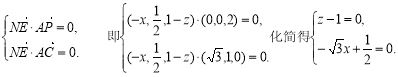 ∴
∴
即![]() 点的坐标为
点的坐标为![]()

练习册系列答案
相关题目