题目内容
【题目】已知数列![]() 的奇数项是公差为
的奇数项是公差为![]() 的等差数列,偶数项是公差为
的等差数列,偶数项是公差为![]() 的等差数列,
的等差数列, ![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和, ![]()
(1)若![]() ,求
,求![]() ;
;
(2)已知![]() ,且对任意的
,且对任意的![]() ,有
,有![]() 恒成立,求证:数列
恒成立,求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() ,且存在正整数
,且存在正整数![]() ,使得
,使得![]() ,求当
,求当![]() 最大时,数列
最大时,数列![]() 的通项公式.
的通项公式.
【答案】(1)14;(2)证明见解析;(3) 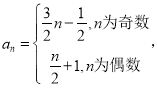
【解析】试题分析:
(1)利用题意求得公差,据此可得a10=14;
(2)结合(1)的结论证得d1=d2=2即可说明数列{an}是等差数列;
(3)分类讨论n的奇偶性即可得到数列的通项公式为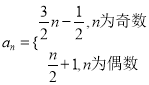 .
.
试题解析:
(1)根据题意,有a1=1,a2=2,a3=a1+d1=1+d1,a4=a2+d2=2+d2,a5=a3+d1=1+2d1∵S5=16,a4=a5
∴a1+a2+a3+a4+a5=7+3d1+d2=16,2+d2=1+2d1∴d1=2, d2=3.
∴a10=2+4d2=14
(2)证明:当n为偶数时,∵an<an+1恒成立,∴![]() ,
,
∴![]()
∴![]() 且d2>1
且d2>1
当n为奇数时,∵an<an+1恒成立,∴![]() ,
,
∴(1n)(d1d2)+2>0
∴![]()
∴d1=d2
∵S15=15a8,∴![]()
∴d1=d2=2
∴an=n
∴数列{an}是等差数列;
(3)若d1=3d2(d1≠0),且存在正整数m、n(m≠n),使得am=an,在m,n中必然一个是奇数,一个是偶数
不妨设m为奇数,n为偶数
∵am=an,∴![]()
∵d1=3d2,∴![]()
∵m为奇数,n为偶数,∴3mn1的最小正值为2,此时d1=3,d2=1
∴数列![]() 的通项公式为
的通项公式为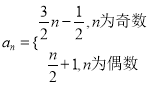 .
.

练习册系列答案
相关题目