题目内容
如图1,矩形 中,
中,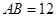 ,
,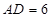 ,
,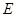 、
、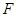 分别为
分别为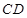 、
、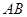 边上的点,且
边上的点,且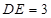 ,
,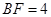 ,将
,将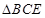 沿
沿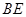 折起至
折起至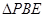 位置(如图2所示),连结
位置(如图2所示),连结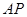 、
、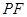 ,其中
,其中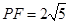 .
.
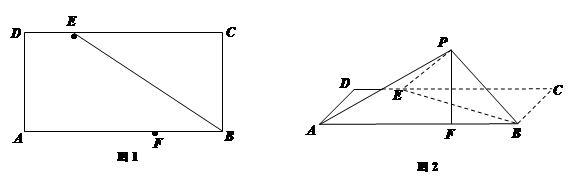
(Ⅰ)求证: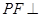 平面
平面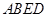 ;
;
(Ⅱ)在线段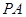 上是否存在点
上是否存在点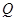 使得
使得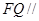 平面
平面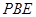 ?若存在,求出点
?若存在,求出点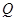 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(Ⅲ)求点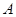 到平面
到平面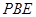 的距离.
的距离.
 中,
中,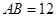 ,
,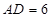 ,
, 、
、 分别为
分别为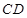 、
、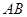 边上的点,且
边上的点,且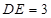 ,
,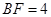 ,将
,将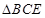 沿
沿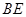 折起至
折起至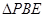 位置(如图2所示),连结
位置(如图2所示),连结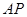 、
、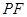 ,其中
,其中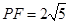 .
.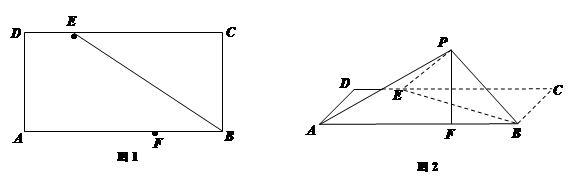
(Ⅰ)求证:
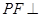 平面
平面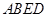 ;
;(Ⅱ)在线段
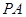 上是否存在点
上是否存在点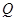 使得
使得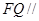 平面
平面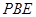 ?若存在,求出点
?若存在,求出点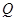 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.(Ⅲ)求点
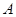 到平面
到平面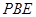 的距离.
的距离.(Ⅰ)答案详见解析;(Ⅱ)存在,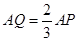 ;(Ⅲ)
;(Ⅲ) 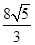 .
.
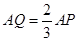 ;(Ⅲ)
;(Ⅲ) 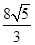 .
.试题分析:(Ⅰ)三角形
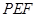 和三角形
和三角形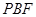 中,各边长度确定,故可利用勾股定理证明垂直关系
中,各边长度确定,故可利用勾股定理证明垂直关系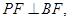
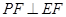 ,进而由线面垂直的判定定理可证明
,进而由线面垂直的判定定理可证明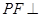 平面
平面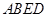 ;(Ⅱ)要使得
;(Ⅱ)要使得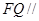 平面
平面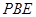 ,只需
,只需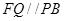 ,因为
,因为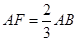 ,故
,故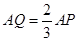 ;(Ⅲ)点到平面的距离,就是点到平面垂线段的长度,如果垂足位置不易确定,可考虑等体积转化,该题中点
;(Ⅲ)点到平面的距离,就是点到平面垂线段的长度,如果垂足位置不易确定,可考虑等体积转化,该题中点 到面
到面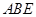 的距离确定,故可利用
的距离确定,故可利用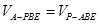 求点
求点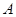 到平面
到平面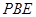 的距离.
的距离.试题解析:(Ⅰ)连结
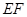 ,由翻折不变性可知,
,由翻折不变性可知,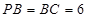 ,
,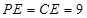 ,在
,在 中,
中,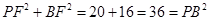 ,所以
,所以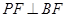 , 在图
, 在图 中,易得
中,易得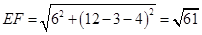 ,
,在
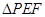 中,
中,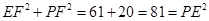 ,所以
,所以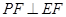 ,又
,又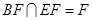 ,
,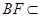 平面
平面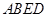 ,
,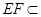 平面
平面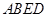 ,所以
,所以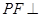 平面
平面 .
.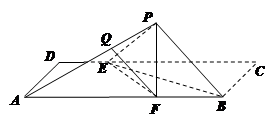
(Ⅱ)当
 为
为 的三等分点(靠近
的三等分点(靠近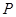 )时,
)时,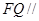 平面
平面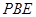 .证明如下:
.证明如下:因为
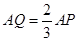 ,
,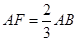 ,所以
,所以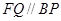 , 又
, 又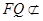 平面
平面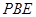 ,
,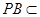 平面
平面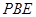 ,所以
,所以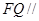 平面
平面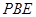 .
.(Ⅲ) 由(Ⅰ)知
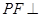 平面
平面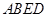 ,所以
,所以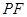 为三棱锥
为三棱锥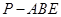 的高.
的高.设点
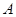 到平面
到平面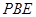 的距离为
的距离为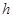 ,由等体积法得
,由等体积法得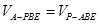 , 即
, 即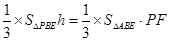 ,又
,又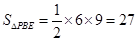 ,
,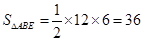 , 所以
, 所以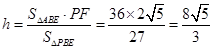 , 即点
, 即点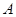 到平面
到平面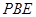 的距离为
的距离为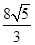 .
.
练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 是正方形,
是正方形,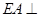 平面
平面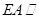
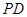 ,
,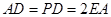 ,
,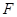 ,
,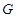 ,
,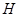 分别为
分别为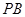 ,
,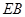 ,
, 的中点.
的中点.

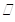 平面
平面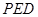 ;
;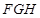 与平面
与平面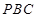 所成锐二面角的大小.
所成锐二面角的大小.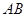 是圆的直径,
是圆的直径,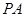 垂直圆所在的平面,
垂直圆所在的平面,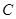 是圆上任一点,
是圆上任一点,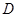 是线段
是线段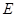 是线段
是线段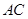 上的一点.
上的一点.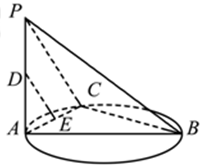
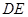 ∥平面
∥平面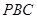 ;
;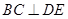 .
. 中,
中, 是边长为
是边长为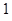 的正方形,
的正方形,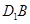 与平面
与平面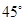 ,则棱
,则棱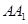 的长为_______;二面角
的长为_______;二面角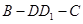 的大小为_______.
的大小为_______.
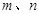 是两条不同的直线,
是两条不同的直线,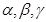 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: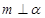 ,
,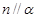 ,则
,则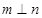
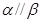 ,
,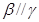 ,
,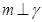
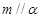 ,
,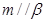 ,
,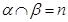 ,则
,则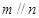
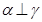 ,
,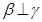 ,
,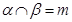 ,则
,则 ,
,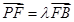 ,若
,若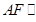 平面BDE,则
平面BDE,则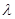 的值为 ( )
的值为 ( )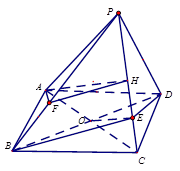
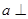 平面
平面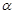 ,直线
,直线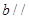 平面
平面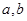 的位置关系是 .
的位置关系是 .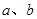 和平面
和平面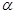 ,下列推论中错误的是( )
,下列推论中错误的是( )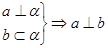
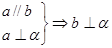
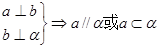
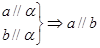
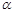 ,
,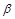 ,
,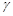 是三个不同的平面,给出下列命题:
是三个不同的平面,给出下列命题: 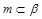 ,
, ,则
,则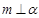 ;
;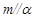 ,
,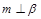 ,则
,则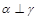 ,则
,则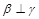 ;
;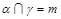 ,
,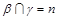 ,
,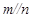 ,则
,则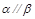 .
.