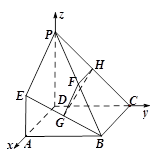
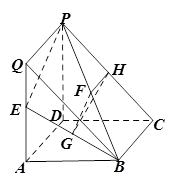
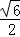题目内容
如图,四边形 是正方形,
是正方形,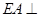 平面
平面 ,
,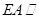
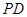 ,
,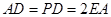 ,
,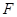 ,
,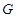 ,
,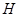 分别为
分别为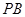 ,
,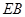 ,
, 的中点.
的中点.

(1)求证:
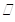 平面
平面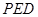 ;
;
(2)求平面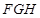 与平面
与平面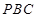 所成锐二面角的大小.
所成锐二面角的大小.
 是正方形,
是正方形,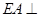 平面
平面 ,
,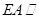
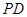 ,
,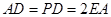 ,
,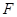 ,
,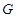 ,
,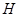 分别为
分别为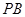 ,
,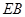 ,
, 的中点.
的中点.
(1)求证:

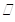 平面
平面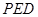 ;
;(2)求平面
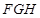 与平面
与平面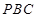 所成锐二面角的大小.
所成锐二面角的大小.(1)证明详见解答;(2)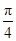 (或
(或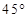 ).
).
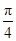 (或
(或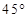 ).
).(1)有单侥幸的中位线定理可证FG∥PE,再根据直线与平面平行的判定定理求证结论即可.
(2)建立适当的空间直角坐标系,写出点的坐标,求出相应向量的的坐标.然后分别出平面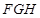 和平面
和平面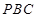 的一个法向量,最后根据向量的夹角公式求得二面角的平面角大小.
的一个法向量,最后根据向量的夹角公式求得二面角的平面角大小.
试题分析:
试题解析:(1)证明: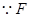 ,
,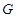 分别为
分别为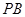 ,
,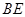 的中点,
的中点,
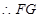
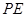 . 1分
. 1分
又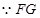
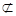 平面
平面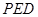 ,
,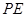
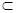 平面
平面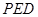 , 3分
, 3分
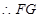
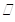 平面
平面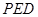 . 5分
. 5分
(2)解: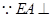 平面
平面 ,
,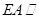
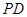 ,
,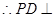 平面
平面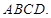
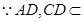 平面
平面
 ,
, .
.
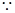 四边形
四边形 是正方形,
是正方形,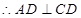 .
.
以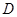 为原点,分别以直线
为原点,分别以直线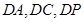 为
为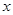 轴,
轴, 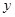 轴,
轴,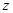 轴
轴
建立如图所示的空间直角坐标系,设 7分
7分
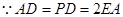 ,
,
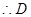
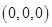 ,
,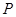
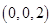 ,
,
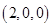 ,
,
 ,
,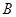
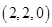 ,
,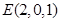 ,
,
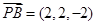 ,
,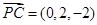 .
.
 ,
, ,
,  分别为
分别为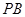 ,
,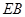 ,
, 的中点,
的中点,
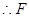
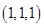 ,
,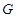
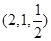 ,
,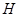
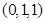 ,
,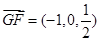 ,
,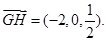 8分
8分
(解法一)设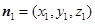 为平面
为平面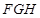 的一个法向量,则
的一个法向量,则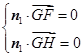 ,
,
即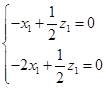 ,令
,令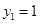 ,得
,得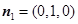 . 10分
. 10分
设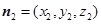 为平面
为平面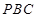 的一个法向量,则
的一个法向量,则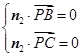 ,
,
即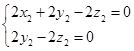 ,令
,令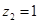 ,得
,得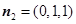 . 12分
. 12分
所以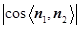 =
=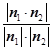 =
=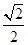 . 13分
. 13分
所以平面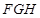 与平面
与平面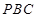 所成锐二面角的大小为
所成锐二面角的大小为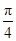 (或
(或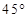 ). 14分
). 14分
(解法二)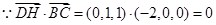 ,
,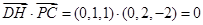 ,
,
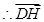 是平面
是平面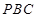 一个法向量. 10分
一个法向量. 10分
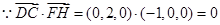 ,
,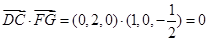 ,
,
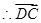 是平面平面
是平面平面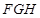 一个法向量. 12分
一个法向量. 12分
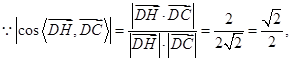 13分
13分
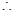 平面
平面 与平面
与平面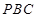 所成锐二面角的大小为
所成锐二面角的大小为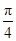 (或
(或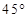 ). 14分
). 14分
(解法三) 延长 到
到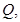 使得
使得 连
连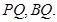
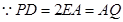 ,
,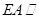
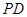 ,
,
 四边形
四边形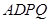 是平行四边形,
是平行四边形,
 四边形
四边形 是正方形,
是正方形,
 ,
,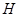 分别为
分别为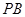 ,
, 的中点,
的中点,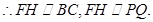
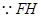
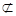 平面
平面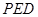 ,
,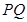
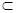 平面
平面 ,
, 
 平面
平面 . 7分
. 7分
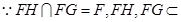 平面
平面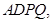
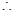 平面
平面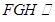 平面
平面 9分
9分
故平面 与平面
与平面 所成锐二面角与二面角
所成锐二面角与二面角 相等. 10分
相等. 10分
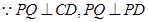
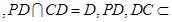 平面
平面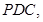
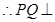 平面
平面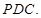
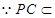 平面
平面
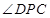 是二面角
是二面角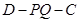 的平面角. 12分
的平面角. 12分
 13分
13分
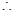 平面
平面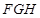 与平面
与平面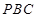 所成锐二面角的大小为
所成锐二面角的大小为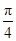 (或
(或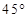 ). 14分
). 14分
(2)建立适当的空间直角坐标系,写出点的坐标,求出相应向量的的坐标.然后分别出平面
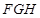 和平面
和平面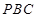 的一个法向量,最后根据向量的夹角公式求得二面角的平面角大小.
的一个法向量,最后根据向量的夹角公式求得二面角的平面角大小.试题分析:
试题解析:(1)证明:
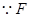 ,
,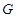 分别为
分别为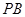 ,
,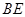 的中点,
的中点,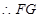
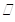
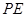 . 1分
. 1分又
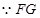
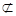 平面
平面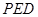 ,
,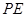
 平面
平面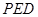 , 3分
, 3分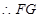
 平面
平面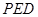 . 5分
. 5分(2)解:
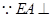 平面
平面 ,
,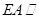
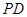 ,
,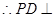 平面
平面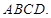
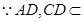 平面
平面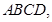
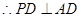 ,
,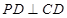 .
. 四边形
四边形 是正方形,
是正方形,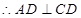 .
.以
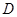 为原点,分别以直线
为原点,分别以直线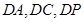 为
为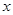 轴,
轴, 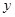 轴,
轴,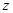 轴
轴建立如图所示的空间直角坐标系,设
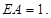 7分
7分
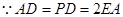 ,
,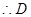
 ,
,
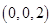 ,
,
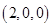 ,
,
 ,
,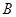
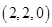 ,
,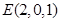 ,
, 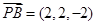 ,
,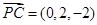 .
.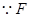 ,
,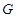 ,
, 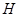 分别为
分别为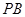 ,
,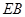 ,
, 的中点,
的中点,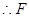
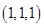 ,
,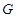
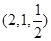 ,
,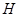
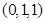 ,
,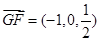 ,
,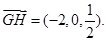 8分
8分(解法一)设
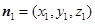 为平面
为平面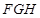 的一个法向量,则
的一个法向量,则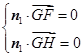 ,
,即
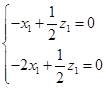 ,令
,令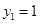 ,得
,得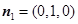 . 10分
. 10分设
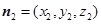 为平面
为平面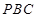 的一个法向量,则
的一个法向量,则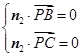 ,
,即
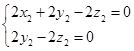 ,令
,令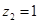 ,得
,得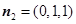 . 12分
. 12分所以
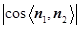 =
=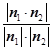 =
=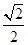 . 13分
. 13分所以平面
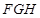 与平面
与平面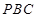 所成锐二面角的大小为
所成锐二面角的大小为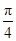 (或
(或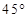 ). 14分
). 14分(解法二)
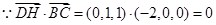 ,
,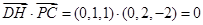 ,
,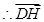 是平面
是平面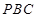 一个法向量. 10分
一个法向量. 10分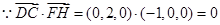 ,
,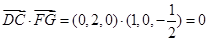 ,
,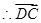 是平面平面
是平面平面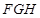 一个法向量. 12分
一个法向量. 12分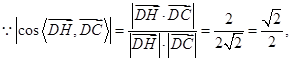 13分
13分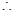 平面
平面 与平面
与平面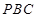 所成锐二面角的大小为
所成锐二面角的大小为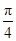 (或
(或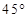 ). 14分
). 14分(解法三) 延长
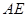 到
到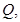 使得
使得 连
连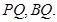

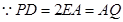 ,
,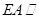
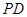 ,
, 四边形
四边形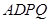 是平行四边形,
是平行四边形,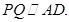
 四边形
四边形 是正方形,
是正方形,
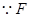 ,
, 分别为
分别为 ,
, 的中点,
的中点,
 平面
平面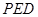 ,
,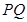
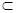 平面
平面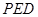 ,
, 
 平面
平面 . 7分
. 7分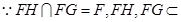 平面
平面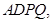
 平面
平面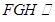 平面
平面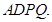 9分
9分故平面
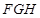 与平面
与平面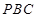 所成锐二面角与二面角
所成锐二面角与二面角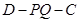 相等. 10分
相等. 10分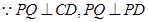
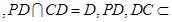 平面
平面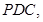
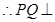 平面
平面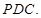
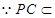 平面
平面
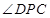 是二面角
是二面角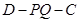 的平面角. 12分
的平面角. 12分 13分
13分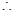 平面
平面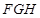 与平面
与平面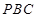 所成锐二面角的大小为
所成锐二面角的大小为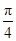 (或
(或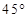 ). 14分
). 14分
练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 中,底面
中,底面 是矩形,四条侧棱长均相等且
是矩形,四条侧棱长均相等且 交
交 于点
于点 .
.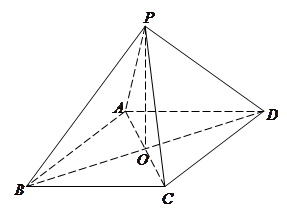
 ;
; .
. 中,
中, ,
, ,
, 、
、 分别为
分别为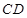 、
、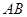 边上的点,且
边上的点,且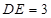 ,
,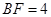 ,将
,将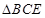 沿
沿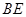 折起至
折起至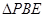 位置(如图2所示),连结
位置(如图2所示),连结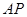 、
、 ,其中
,其中 .
.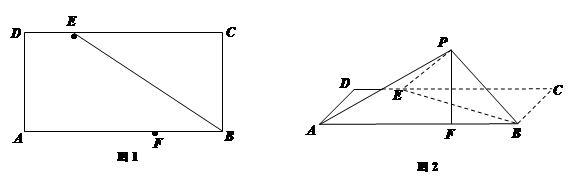
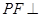 平面
平面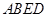 ;
;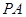 上是否存在点
上是否存在点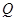 使得
使得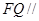 平面
平面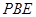 ?若存在,求出点
?若存在,求出点 到平面
到平面 的底面是正方形,
的底面是正方形,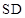 ⊥平面
⊥平面 ,
,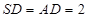
 ;
; 的大小.
的大小.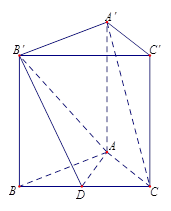
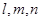 是三条互不相同的空间直线,
是三条互不相同的空间直线,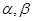 是两个不重合的平面,
是两个不重合的平面,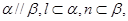 则
则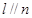 ; ②若
; ②若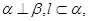 则
则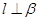 ;
;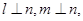 则
则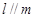 ; ④若
; ④若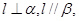 则
则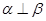
 和两个不同的平面
和两个不同的平面 ,则下列命题正确的是( )
,则下列命题正确的是( ) 则
则
 则
则
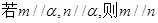
 则
则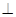 平面
平面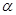 ,直线
,直线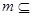 平面
平面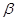 ,则下列四个结论:
,则下列四个结论: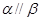 ,则
,则 ②若
②若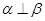 ,则
,则