题目内容
已知函数f(x)=x2-2acos kπ·ln x(k∈N*,a∈R,且a>0).
(1)讨论函数f(x)的单调性;
(2)若k=2 04,关于x的方程f(x)=2ax有唯一解,求a的值.
(1)讨论函数f(x)的单调性;
(2)若k=2 04,关于x的方程f(x)=2ax有唯一解,求a的值.
(1)当k是奇数时,f′(x)>0,则f(x)在(0,+∞)上是增函数;
当k是偶数时,f(x)在(0,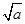 )上是单调减函数,在(
)上是单调减函数,在(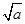 ,+∞)上是单调增函数.
,+∞)上是单调增函数.
(2)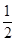
当k是偶数时,f(x)在(0,
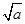 )上是单调减函数,在(
)上是单调减函数,在(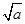 ,+∞)上是单调增函数.
,+∞)上是单调增函数.(2)
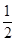
解:(1)由已知得x>0
且f′(x)=2x-(-1)k·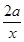 .
.
当k是奇数时,f′(x)>0,
则f(x)在(0,+∞)上是增函数;
当k是偶数时,
则f′(x)=2x-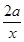 =
=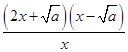 .
.
所以当x∈(0,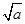 )时,f′(x)<0;
)时,f′(x)<0;
当x∈(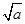 ,+∞)时,f′(x)>0.
,+∞)时,f′(x)>0.
故当k是偶数时,f(x)在(0,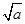 )上是单调减函数,在(
)上是单调减函数,在(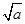 ,+∞)上是单调增函数.
,+∞)上是单调增函数.
(2)若k=2 014,
则f(x)=x2-2aln x(k∈N*).
记g(x)=f(x)-2ax=x2-2aln x-2ax,
则g′(x)=2x-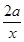 -2a=
-2a=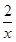 (x2-ax-a).
(x2-ax-a).
则方程f(x)=2ax有唯一解,即g(x)=0有唯一解.
令g′(x)=0,得x2-ax-a=0.
因为a>0,x>0,
所以x1=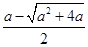 <0(舍去),
<0(舍去),
x2=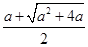 .
.
当x∈(0,x2)时,g′(x)<0,g(x)在(0,x2)上是单调减函数;当x∈(x2,+∞)时,g′(x)>0,g(x)在(x2,+∞)上是单调增函数.
当x=x2时,g′(x2)=0,g(x)min=g(x2).
因为g(x)=0有唯一解,所以g(x2)=0.则
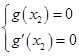 ,即
,即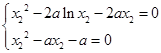
两式相减得2aln x2+ax2-a=0,
因为a>0,所以2ln x2+x2-1=0.(*)
设函数h(x)=2lnx+x-1.
因为当x>0时,h(x)是增函数,所以h(x)=0至多有一个解.
因为h(1)=0,所以方程(*)的解为x2=1.
从而解得a=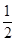 .
.
且f′(x)=2x-(-1)k·
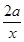 .
.当k是奇数时,f′(x)>0,
则f(x)在(0,+∞)上是增函数;
当k是偶数时,
则f′(x)=2x-
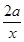 =
=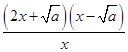 .
.所以当x∈(0,
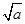 )时,f′(x)<0;
)时,f′(x)<0;当x∈(
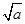 ,+∞)时,f′(x)>0.
,+∞)时,f′(x)>0.故当k是偶数时,f(x)在(0,
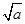 )上是单调减函数,在(
)上是单调减函数,在(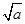 ,+∞)上是单调增函数.
,+∞)上是单调增函数.(2)若k=2 014,
则f(x)=x2-2aln x(k∈N*).
记g(x)=f(x)-2ax=x2-2aln x-2ax,
则g′(x)=2x-
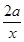 -2a=
-2a=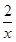 (x2-ax-a).
(x2-ax-a).则方程f(x)=2ax有唯一解,即g(x)=0有唯一解.
令g′(x)=0,得x2-ax-a=0.
因为a>0,x>0,
所以x1=
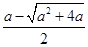 <0(舍去),
<0(舍去),x2=
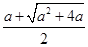 .
.当x∈(0,x2)时,g′(x)<0,g(x)在(0,x2)上是单调减函数;当x∈(x2,+∞)时,g′(x)>0,g(x)在(x2,+∞)上是单调增函数.
当x=x2时,g′(x2)=0,g(x)min=g(x2).
因为g(x)=0有唯一解,所以g(x2)=0.则
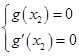 ,即
,即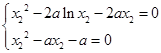
两式相减得2aln x2+ax2-a=0,
因为a>0,所以2ln x2+x2-1=0.(*)
设函数h(x)=2lnx+x-1.
因为当x>0时,h(x)是增函数,所以h(x)=0至多有一个解.
因为h(1)=0,所以方程(*)的解为x2=1.
从而解得a=
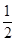 .
.
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
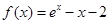 ,则函数
,则函数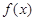 的零点所在区间为( )
的零点所在区间为( )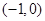
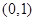
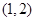
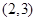
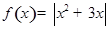 ,
,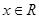 .若方程
.若方程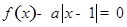 恰有4个互异的实数根,则实数
恰有4个互异的实数根,则实数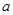 的取值范围为__________.
的取值范围为__________. )x-sinx在区间[0,2π]上的零点个数为( )
)x-sinx在区间[0,2π]上的零点个数为( )
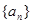 和等比数列
和等比数列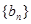 的首项均为1,且公差
的首项均为1,且公差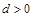 ,公比
,公比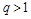 ,则集合
,则集合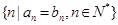 的元素个数最多有 个.
的元素个数最多有 个.