题目内容
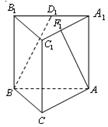
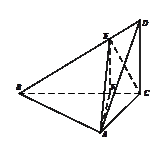
(本题满分14分) 如图,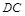 垂直平面
垂直平面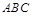 ,
,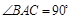 ,
,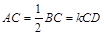 ,点
,点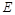 在
在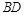 上,且
上,且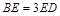 .
.
(Ⅰ)求证: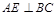 ;
;
(Ⅱ)若二面角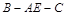 的大小为
的大小为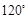 ,求
,求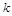 的值.
的值.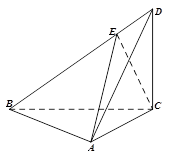
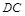 垂直平面
垂直平面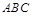 ,
,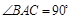 ,
,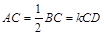 ,点
,点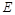 在
在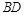 上,且
上,且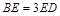 .
.(Ⅰ)求证:
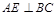 ;
;(Ⅱ)若二面角
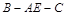 的大小为
的大小为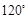 ,求
,求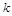 的值.
的值.
见解析
解:(Ⅰ)过E点作EF AB与点F,连AF,于是EF//DC
AB与点F,连AF,于是EF//DC
所以EF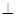 ABC,又BC
ABC,又BC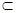 ABC,所以EF
ABC,所以EF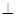 BC;
BC;
又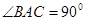 ,AC=1/2BC,所以
,AC=1/2BC,所以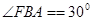 ,所以
,所以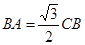 ,
,
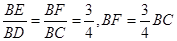 ,所以
,所以
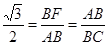 ,所以
,所以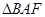 与
与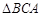 相似,所以
相似,所以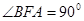 ,即AF
,即AF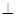 BC;又AF
BC;又AF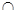 EF=F,于是BC
EF=F,于是BC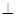 AEF,又AE
AEF,又AE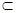 AFE,
AFE,
所以BC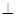 AE. ……6′
AE. ……6′
(2)解法一(空间向量法)
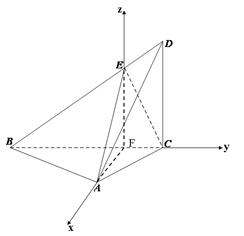
如右图,以F为原点,FA为x轴,FC为y轴,FE为z轴,建立空间直角坐标系,则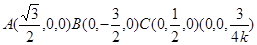 ,于是
,于是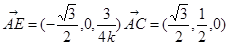 ,,
,,
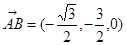 ,设平面ABE的法向量为
,设平面ABE的法向量为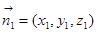 ,
,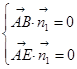 ,于是,令Z1=1,得
,于是,令Z1=1,得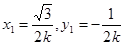 ,得
,得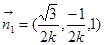 .
.
设平面ACE的法向量为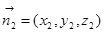 ,
,
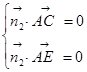 ,于是,令Z2=1,得
,于是,令Z2=1,得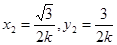 ,得
,得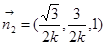 .
.
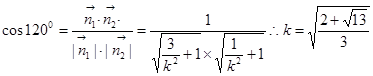 ……8′
……8′
思路分析:第一问中利用线面垂直 的判定定理和性质定理求证即可。
第二问中,如右图,以F为原点,FA为x轴,FC为y轴,FE为z轴,建立空间直角坐标系,则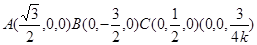 ,于是
,于是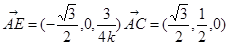 ,,建立空间直角坐标系,然后表示平面的法向量的夹角得到k的值。
,,建立空间直角坐标系,然后表示平面的法向量的夹角得到k的值。
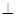 AB与点F,连AF,于是EF//DC
AB与点F,连AF,于是EF//DC
所以EF
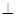 ABC,又BC
ABC,又BC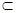 ABC,所以EF
ABC,所以EF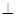 BC;
BC;又
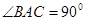 ,AC=1/2BC,所以
,AC=1/2BC,所以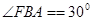 ,所以
,所以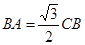 ,
,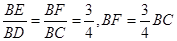 ,所以
,所以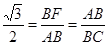 ,所以
,所以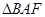 与
与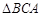 相似,所以
相似,所以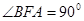 ,即AF
,即AF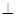 BC;又AF
BC;又AF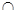 EF=F,于是BC
EF=F,于是BC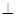 AEF,又AE
AEF,又AE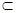 AFE,
AFE,所以BC
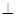 AE. ……6′
AE. ……6′ (2)解法一(空间向量法)
如右图,以F为原点,FA为x轴,FC为y轴,FE为z轴,建立空间直角坐标系,则
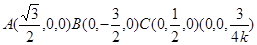 ,于是
,于是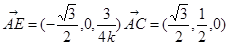 ,,
,, 
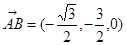 ,设平面ABE的法向量为
,设平面ABE的法向量为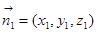 ,
,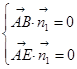 ,于是,令Z1=1,得
,于是,令Z1=1,得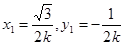 ,得
,得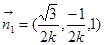 .
.设平面ACE的法向量为
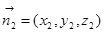 ,
,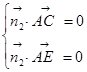 ,于是,令Z2=1,得
,于是,令Z2=1,得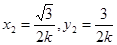 ,得
,得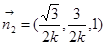 .
.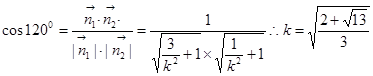 ……8′
……8′ 思路分析:第一问中利用线面垂直 的判定定理和性质定理求证即可。
第二问中,如右图,以F为原点,FA为x轴,FC为y轴,FE为z轴,建立空间直角坐标系,则
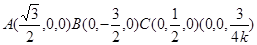 ,于是
,于是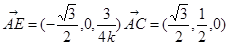 ,,建立空间直角坐标系,然后表示平面的法向量的夹角得到k的值。
,,建立空间直角坐标系,然后表示平面的法向量的夹角得到k的值。
练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
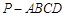 的底面ABCD为正方形,
的底面ABCD为正方形,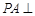 平面ABCD,E、F分别是BC,PC的中点,
平面ABCD,E、F分别是BC,PC的中点,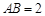 ,
,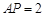 .
.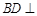 平面
平面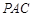 ;
;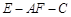 的大小.
的大小.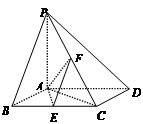
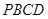 ,
,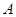 为
为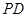 上一点,且
上一点,且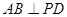 ,
,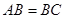 ,
,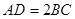 ,沿着
,沿着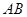 折叠使得二面角
折叠使得二面角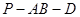 为
为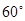 的二面角,连结
的二面角,连结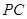 、
、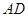 上取一点
上取一点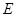 使得
使得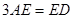 ,连结
,连结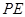 得到如下图(图2)的一个几何体.
得到如下图(图2)的一个几何体.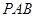
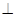 平面
平面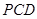 ;
;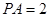 ,求点
,求点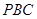 的距离.
的距离.
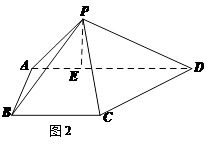
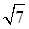 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过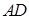 作圆柱的截面交下底面于
作圆柱的截面交下底面于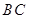 .
.
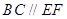 ;
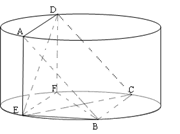
;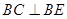 ;
;
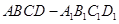 中,底面
中,底面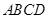 是边长为
是边长为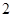 的正方形,
的正方形,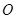 为
为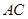 与
与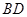 的交点,
的交点,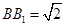 ,
,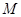 是线段
是线段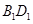 的中点.
的中点.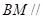 平面
平面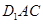 ;
;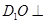 平面
平面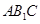 ;
;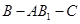 的大小.
的大小.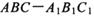 中,.
中,.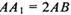 ,M为CC1的中点,则直线BM与平面
,M为CC1的中点,则直线BM与平面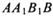 所成角的正弦值是_________.
所成角的正弦值是_________.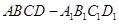 .则下列四个命题
.则下列四个命题
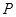 在直线
在直线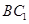 上运动时,三棱锥
上运动时,三棱锥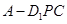 的体积不变;
的体积不变;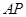 与平面
与平面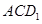 所成的角的大小不变;
所成的角的大小不变;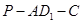 的大小不变;
的大小不变;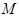 是平面
是平面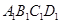 上到点
上到点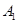 和
和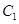 距离相等的点,则
距离相等的点,则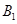
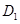 ;
;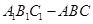 是直三棱柱,
是直三棱柱,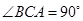 ,点
,点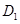 、
、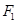 分别是
分别是 ,
,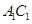 的中点,若
的中点,若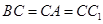 ,则
,则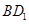 与
与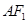 所成角的余弦值为
所成角的余弦值为