题目内容
(本小题满分12分)如下图(图1)等腰梯形 ,
, 为
为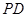 上一点,且
上一点,且 ,
,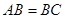 ,
, ,沿着
,沿着 折叠使得二面角
折叠使得二面角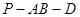 为
为 的二面角,连结
的二面角,连结 、
、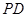 ,在
,在 上取一点
上取一点 使得
使得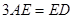 ,连结
,连结 得到如下图(图2)的一个几何体.
得到如下图(图2)的一个几何体.
(Ⅰ)求证:平面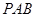
 平面
平面 ;
;
(Ⅱ)设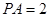 ,求点
,求点 到平面
到平面 的距离.
的距离.

 ,
, 为
为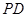 上一点,且
上一点,且 ,
,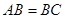 ,
, ,沿着
,沿着 折叠使得二面角
折叠使得二面角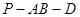 为
为 的二面角,连结
的二面角,连结 、
、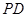 ,在
,在 上取一点
上取一点 使得
使得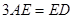 ,连结
,连结 得到如下图(图2)的一个几何体.
得到如下图(图2)的一个几何体.(Ⅰ)求证:平面
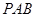
 平面
平面 ;
;(Ⅱ)设
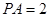 ,求点
,求点 到平面
到平面 的距离.
的距离.

(Ⅰ)证明:见解析; (Ⅱ)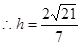
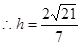
(1)解决本小题关键是根据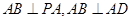 ,又二面角P-AB-D为
,又二面角P-AB-D为 ,
,
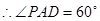 ,又AD=2PA,
,又AD=2PA,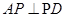 .
.
(2)本小题可根据体积法利用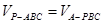 求E到平面PBC的距离.
求E到平面PBC的距离.
(Ⅰ)证明: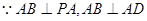 ,又二面角P-AB-D为
,又二面角P-AB-D为
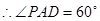 ,又AD=2PA
,又AD=2PA 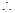
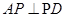
有平面图形易知:AB 平面APD,又
平面APD,又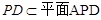 ,
,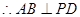 ,
,
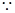
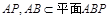 ,且
,且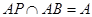
 ,又
,又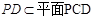 ,
,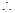 平面PAB
平面PAB 平面PCD ……………6分
平面PCD ……………6分
(Ⅱ)设E到平面PBC的距离为 ,
, 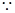 AE//平面PBC
AE//平面PBC
所以A 到平面PBC的距离亦为 , 连结AC,则
, 连结AC,则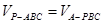 ,
,
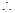
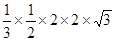 =
=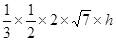
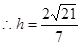 ………………………12分
………………………12分
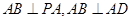 ,又二面角P-AB-D为
,又二面角P-AB-D为 ,
,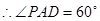 ,又AD=2PA,
,又AD=2PA,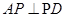 .
.(2)本小题可根据体积法利用
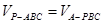 求E到平面PBC的距离.
求E到平面PBC的距离.(Ⅰ)证明:
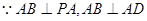 ,又二面角P-AB-D为
,又二面角P-AB-D为
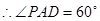 ,又AD=2PA
,又AD=2PA 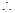
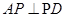
有平面图形易知:AB
 平面APD,又
平面APD,又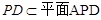 ,
,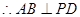 ,
,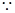
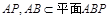 ,且
,且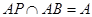
 ,又
,又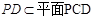 ,
,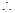 平面PAB
平面PAB 平面PCD ……………6分
平面PCD ……………6分(Ⅱ)设E到平面PBC的距离为
 ,
, 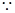 AE//平面PBC
AE//平面PBC所以A 到平面PBC的距离亦为
 , 连结AC,则
, 连结AC,则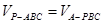 ,
,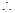
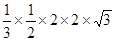 =
=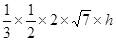
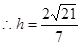 ………………………12分
………………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,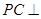 底面
底面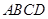 ,
,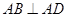 ,
,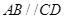 ,
,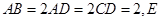 是
是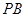 的中点。
的中点。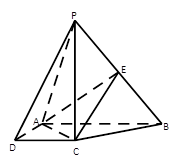
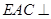 平面
平面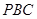 (4分)
(4分)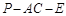 的余弦值为
的余弦值为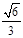 ,求直线
,求直线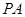 与平面
与平面 所成角的正弦值.(8分)
所成角的正弦值.(8分)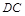 垂直平面
垂直平面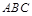 ,
,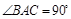 ,
,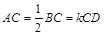 ,点
,点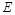 在
在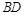 上,且
上,且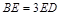 .
.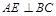 ;
;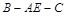 的大小为
的大小为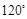 ,求
,求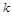 的值.
的值.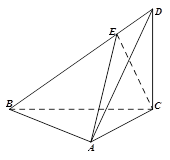
 。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
。AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.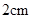 的圆柱器皿中(底面水平放置),量得水面的高度为
的圆柱器皿中(底面水平放置),量得水面的高度为 .若将这些水倒入轴截面是正三角形的倒置的圆锥形器皿中,则水面的高度是( )
.若将这些水倒入轴截面是正三角形的倒置的圆锥形器皿中,则水面的高度是( )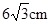
 为端点的三条棱长都等于1,且它们彼此的夹角都是
为端点的三条棱长都等于1,且它们彼此的夹角都是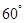 ,那么以这个顶点为端点的晶体的对角线的长为 。
,那么以这个顶点为端点的晶体的对角线的长为 。