题目内容
设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=2x2.(Ⅰ) 求x<0时,f(x)的表达式;
(Ⅱ) 令g(x)=lnx,问是否存在x,使得f(x),g(x)在x=x处的切线互相平行?若存在,请求出x值;若不存在,请说明理由.
【答案】分析:(Ⅰ)先取x<0,-x>0,再由奇函数的性质f(x)=-f(-x)及x≥0时,f(x)=2x2.求出解析式即可
(Ⅱ)求出两个函数的导数,令f'(x)=g'(x),若此方程有根,则说明存在,否则说明不存在
解答:解:(Ⅰ)当x<0时,-x>0,f(x)=-f(-x)=-2(-x)2=-2x2;(6分)
(Ⅱ)若f(x),g(x)在x处的切线互相平行,则f'(x)=g'(x),(4分)
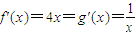 ,解得,
,解得,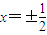
∵x≥0,得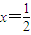 (4分)
(4分)
点评:本题考查奇函数,求解本题的关键是根据奇函数的性质得到方程解出x<0时,f(x)的表达式,熟练掌握导数的几何意义,建立导数的方程求方程的根,以此来确定这样的直线存在与否.
(Ⅱ)求出两个函数的导数,令f'(x)=g'(x),若此方程有根,则说明存在,否则说明不存在
解答:解:(Ⅰ)当x<0时,-x>0,f(x)=-f(-x)=-2(-x)2=-2x2;(6分)
(Ⅱ)若f(x),g(x)在x处的切线互相平行,则f'(x)=g'(x),(4分)
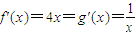 ,解得,
,解得,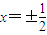
∵x≥0,得
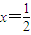 (4分)
(4分)点评:本题考查奇函数,求解本题的关键是根据奇函数的性质得到方程解出x<0时,f(x)的表达式,熟练掌握导数的几何意义,建立导数的方程求方程的根,以此来确定这样的直线存在与否.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |