题目内容
【题目】已知函数
，
，若函数
有三个不同的零点
，
，
（其中
），则
的取值范围为__________．
【答案】
【解析】如图：
，
，作出函数图象如图所示
，
，作出函数图象如图所示
，由
有三个不同的零点
，如图
令
得
为满足有三个零点，如图可得
，
点睛：本题考查了函数零点问题，先由导数求出两个函数的单调性，继而画出函数图像，再由函数的零点个数确定参量取值范围，将问题转化为函数的两根问题来求解，本题需要化归转化，函数的思想，零点问题等较为综合，有很大难度。
【题型】填空题
【结束】
17
【题目】已知等比数列
的前
项和为
，且满足
.
（1）求数列
的通项公式；
（2）若数列
满足
，求数列
的前
项和
.
【答案】（1）
；（2）
【解析】试题分析： 
法一：根据
即可求出数列
的通项公式；法二：根据等比数列的前
项和公式和已知条件求出公比
和首项
的值，即可求出数列
的通项公式； 
根据对数的运算性质求出
，代入即可求出的数列
的通项公式，利用裂项法求出数列
的前
项和
解析：(1)
法一：由
得
，
当
时， 
，即
，
又
，当
时符合上式，所以通项公式为
.
法二：由
得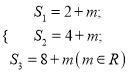
，
从而有
，
所以等比数列公比
，首项
，因此通项公式为
.
（2）由（1）可得
，
，
.
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
