题目内容
【题目】已知等比数列![]() 的公比
的公比![]() ,前
,前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.![]() ,
,![]() ,
,![]() 分别是一个等差数列的第1项,第2项,第5项.
分别是一个等差数列的第1项,第2项,第5项.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() ,
,![]() 的前
的前![]() 项和为
项和为![]() ,且对任意的
,且对任意的![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() . (2)
. (2) ![]() ;(3)
;(3) ![]()
【解析】
(1)利用等比数列通项公式以及求和公式化简![]() ,得到
,得到![]() ,由
,由![]() ,
,![]() ,
,![]() 分别是一个等差数列的第1项,第2项,第5项,利用等差数列的定义可得
分别是一个等差数列的第1项,第2项,第5项,利用等差数列的定义可得![]() ,化简即可求出
,化简即可求出![]() ,从而得到数列
,从而得到数列![]() 的通项公式。
的通项公式。
(2)由(1)可得![]() ,利用错位相减,求出数列
,利用错位相减,求出数列![]() 的前
的前![]() 项和
项和![]() 即可;
即可;
(3)结合(1)可得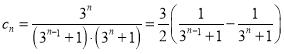 ,利用裂项相消法,即可得到
,利用裂项相消法,即可得到![]() 的前
的前![]() 项和
项和![]() ,求出
,求出![]() 的最大值,即可解得实数
的最大值,即可解得实数![]() 的取值范围
的取值范围
(1)由![]() 得
得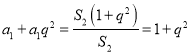 ,所以
,所以![]() ,
,
由![]() ,
,![]() ,
,![]() 分别是一个等差数列的第1项,第2项,第5项,
分别是一个等差数列的第1项,第2项,第5项,
得![]() ,
,
即![]() ,
,
即![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(2)由于![]() ,所以
,所以![]() ,
,
所以![]() ,
,
![]() ,
,
两式相减得,![]() ,
,
所以![]()
(3)由![]() 知
知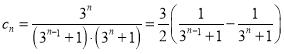 ,
,
∴![]()
![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() .
.
即实数![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
