题目内容
5.若直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则$\frac{1}{a}+\frac{1}{b}$的最小值是( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | 4 |
分析 由题意可得2ax-by+2=0(a>0,b>0)经过圆心,可得a+b=1,则$\frac{1}{a}+\frac{1}{b}$=$\frac{a+b}{a}$+$\frac{a+b}{b}$=2+$\frac{b}{a}$+$\frac{a}{b}$,再利用基本不等式求得它的最小值.
解答 解:圆x2+y2+2x-4y+1=0,即(x+1)2+(y-2)2 =4,表示以(-1,2)为圆心、半径等于2的圆.
再根据弦长为4,可得2ax-by+2=0(a>0,b>0)经过圆心,故有-2a-2b+2=0,
求得a+b=1,则$\frac{1}{a}+\frac{1}{b}$=$\frac{a+b}{a}$+$\frac{a+b}{b}$=2+$\frac{b}{a}$+$\frac{a}{b}$≥4,当且仅当a=b=$\frac{1}{2}$时,取等号,
故则$\frac{1}{a}+\frac{1}{b}$的最小值为4,
故选:D.
点评 本题主要考查直线和圆的位置关系,基本不等式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列程序的功能是( )
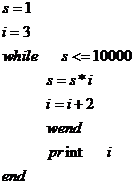
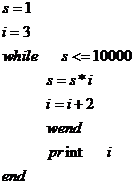
| A. | 求1×2×3×4×…×10 000的值 | |
| B. | 求2×4×6×8×…×10 000的值 | |
| C. | 求3×5×7×9×…×10 000的值 | |
| D. | 求满足1×3×5×…×n>10 000的最小正整数n |
20.复数$\frac{i-1}{i}$(i是虚数单位)在复平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$的面积是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |