题目内容
17.已知函数f(x)=ax2+x-a,若f(x)有最大值$\frac{17}{8}$,(1)求实数a的值;
(2)解不等式f(x)>1.
分析 (1)根据f(x)有最大值,即可判断出a<0,并且$\frac{-4{a}^{2}-1}{4a}=\frac{17}{8}$,解该方程即得a的值,a=$-\frac{1}{8}$,或a=-2;
(2)分别将a的这两个值带人不等式f(x)>1,即可得到两个一元二次不等式,分别解这两个不等式即得原不等式的解.
解答 解:(1)若a=0,f(x)=x无最大值;
∴a≠0;
∴f(x)是二次函数,且a<0;
∴f(x)的最大值为$\frac{-4{a}^{2}-1}{4a}=\frac{17}{8}$;
解得a=$-\frac{1}{8}$,或a=-2;
(2)①当a=$-\frac{1}{8}$时,f(x)=$-\frac{1}{8}{x}^{2}+x+\frac{1}{8}$;
∴解$-\frac{1}{8}{x}^{2}+x+\frac{1}{8}>1$得,1<x<7;
∴f(x)>1的解集为(1,7);
②当a=-2时,f(x)=-2x2+x+2;
∴解-2x2+x+2>1得,$-\frac{1}{2}<x<1$;
∴f(x)>1的解集为(-$\frac{1}{2}$,1).
点评 考查二次函数在定义域R上的最大值,以及计算二次函数最大值的公式,解一元二次不等式.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
5.若直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则$\frac{1}{a}+\frac{1}{b}$的最小值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | 4 |
12.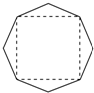 某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成.该八边形的面积为( )
某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成.该八边形的面积为( )
 某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成.该八边形的面积为( )
某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成.该八边形的面积为( )| A. | 2sin α-2cos α+2 | B. | sin α-$\sqrt{3}$cos α+3 | C. | 3sin α-$\sqrt{3}$cos α+1 | D. | 2sin α-cos α+1 |
2.不等式$\frac{x-1}{{x}^{2}-4}$>0的解集是( )
| A. | (-2,1)∪(2,+∞) | B. | (2,+∞) | C. | (-2,1) | D. | (-∞,-2)∪(1,+∞) |

 如图是三棱柱被平面截去一部分后剩余的几何体的三视图,则截掉的几何体与三视图所示的几何体的体积之比为1:2.
如图是三棱柱被平面截去一部分后剩余的几何体的三视图,则截掉的几何体与三视图所示的几何体的体积之比为1:2.