题目内容
【题目】已知cosα= ![]() ,cos(α﹣β)=
,cos(α﹣β)= ![]() ,且0<β<α<
,且0<β<α< ![]() ,
,
(1)求tanα的值;
(2)求β.
【答案】
(1)解:因为cosα= ![]() ,cos(α﹣β)=
,cos(α﹣β)= ![]() ,且0<β<α<
,且0<β<α< ![]() ,∴α﹣β>0
,∴α﹣β>0
所以sinα= ![]() =
= ![]() ,
,
∴ 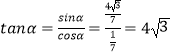
(2)解:cos(α﹣β)= ![]() ,且0<β<α<
,且0<β<α< ![]() ,∴α﹣β>0,
,∴α﹣β>0,
α﹣β∈(0, ![]() ),
),
∴sin(α﹣β)= ![]() =
= ![]() =
= ![]() ,
,
cosβ=cos[(α﹣(α﹣β)]=cosαcos(α﹣β)+sinαsin(α﹣β)
= ![]() ×
× ![]() =
= ![]() ,
,
∵0<β<α< ![]() ,∴
,∴ ![]()
【解析】(1)通过α、β的范围,利用同角三角函数的基本关系式求出sinα,然后求出tanα.(2)求出α﹣β的范围,然后求出sinα,sin(α﹣β)的值,即可求解cosβ.然后求出β值.
【考点精析】认真审题,首先需要了解两角和与差的余弦公式(两角和与差的余弦公式:![]() ).
).

练习册系列答案
相关题目