题目内容
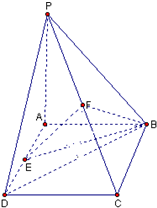 (2008•湖北模拟)如图,在四棱锥P-ABCD中,底面是矩形,且AD=
(2008•湖北模拟)如图,在四棱锥P-ABCD中,底面是矩形,且AD=| 2 |
(1)求证:EF为AD及PC的公垂线(2)求直线BD与平面BEF所成的角.
分析:方法一:(1)利用空间向量,欲证EF为AD及PC的公垂线,因为E,F两点分别在AD,PC上,只需证明
•
=0,
•
=0,建立空间直角坐标系,用向量的数量积公式计算即可.
(2)欲求直线BD与平面BEF所成的角,只需把求出EF的方向向量与平面BEF的法向量所成的角,则求直线BD与平面BEF所成的角等于该角或其补角.
方法二:(1)欲证EF为AD及PC的公垂线,因为E,F两点分别在AD,PC上,只需证明EF⊥PC,EF⊥AD,连接FO、OE、EP、EC,通过够造的三角形EPC为等腰三角形,证明EF⊥PC,利用三垂线定理证明EF⊥AD.
(2)欲求直线BD与平面BEF所成的角,只需找到直线BD在平面BEF上的射影,则BD与它的射影所成角即为所求.过O作OH⊥平面EFB于H,连BH,∠OBH为所求BD与平面EFB所成的角,再利用等体积法求出OH即可.
| AD |
| EF |
| PC |
| EF |
(2)欲求直线BD与平面BEF所成的角,只需把求出EF的方向向量与平面BEF的法向量所成的角,则求直线BD与平面BEF所成的角等于该角或其补角.
方法二:(1)欲证EF为AD及PC的公垂线,因为E,F两点分别在AD,PC上,只需证明EF⊥PC,EF⊥AD,连接FO、OE、EP、EC,通过够造的三角形EPC为等腰三角形,证明EF⊥PC,利用三垂线定理证明EF⊥AD.
(2)欲求直线BD与平面BEF所成的角,只需找到直线BD在平面BEF上的射影,则BD与它的射影所成角即为所求.过O作OH⊥平面EFB于H,连BH,∠OBH为所求BD与平面EFB所成的角,再利用等体积法求出OH即可.
解答:解;方法一:
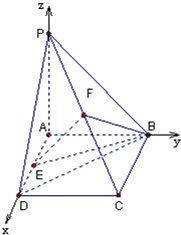 设AB=1,则AD=
设AB=1,则AD=
(1)A(0,0,0)B(0,1,0)C(
,1,0)D(
,0,0)E(
,0,0)P(0,0,1)F(
,
,
)
=(
,0,0)
=(
,1,-1)
=(0,
,
)
∴
•
=0
•
=-
+
=0
∴AD⊥EF PC⊥EF
故PC为AD及EF的公垂线
(2)
=(-
,1,0)
•
=-1+1+0=0
∴PC⊥EB∴PC⊥平面EFB故
可看成平面EFB的法向量
故sinα=
=
=
方法二:
(1)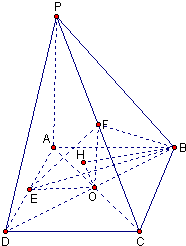 连FO、OE、EP、EC∵EP2=EA2+AP2 EC2=ED2+CD2
连FO、OE、EP、EC∵EP2=EA2+AP2 EC2=ED2+CD2
又∵AB=AP=CD EA=ED∴EP=EC
又∵F为PC的中点∴EF⊥PC
又∵OF∥AP∴OF⊥平面ABCD
而OE⊥AD∴EF⊥AD
故EF为AD及PC的公垂线
(2)过O作OH⊥平面EFB于H,连BH,∠OBH为所求BD与平面EFB所成的角
设AD=
AB=1EF2=(
)2+(
)2=
BF2=(
)2+(
)2=1
∴EF2+BF2=BE2∴VO-EFB=VF-OEB
×
×
×1×OH=
×
×
×
×
∴OH=
sin∠OBH=
=
 设AB=1,则AD=
设AB=1,则AD=| 2 |
(1)A(0,0,0)B(0,1,0)C(
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AD |
| 2 |
| PC |
| 2 |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AD |
| EF |
| PC |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
∴AD⊥EF PC⊥EF
故PC为AD及EF的公垂线
(2)
| EB |
| ||
| 2 |
| PC |
| EB |
∴PC⊥EB∴PC⊥平面EFB故
| PC |
故sinα=
| ||||
|
|
| 2-1 | ||
2×
|
| ||
| 6 |
方法二:
(1)
 连FO、OE、EP、EC∵EP2=EA2+AP2 EC2=ED2+CD2
连FO、OE、EP、EC∵EP2=EA2+AP2 EC2=ED2+CD2又∵AB=AP=CD EA=ED∴EP=EC
又∵F为PC的中点∴EF⊥PC
又∵OF∥AP∴OF⊥平面ABCD
而OE⊥AD∴EF⊥AD
故EF为AD及PC的公垂线
(2)过O作OH⊥平面EFB于H,连BH,∠OBH为所求BD与平面EFB所成的角
设AD=
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴EF2+BF2=BE2∴VO-EFB=VF-OEB
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴OH=
| 1 |
| 4 |
| ||||
|
| ||
| 6 |
点评:本题主要考查了两异面直线公垂线的判断,以及直线与平面所成角的求法,综合考查了学生的识图能力,空间想象力,计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2008•湖北模拟)已知向量
(2008•湖北模拟)已知向量