题目内容
设数列{an}的各项都是正数,且对任意n∈N*,都有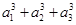 +…+
+…+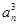 =
=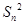 ,记Sn为数列{an}的前n项和.
,记Sn为数列{an}的前n项和.
(1)求数列{an}的通项公式;
(2)若bn=3n+(-1)n-1λ·2an(λ为非零常数,n∈N*),问是否存在整数λ,使得对任意n∈N*,都有bn+1>bn.
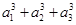 +…+
+…+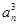 =
=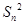 ,记Sn为数列{an}的前n项和.
,记Sn为数列{an}的前n项和.(1)求数列{an}的通项公式;
(2)若bn=3n+(-1)n-1λ·2an(λ为非零常数,n∈N*),问是否存在整数λ,使得对任意n∈N*,都有bn+1>bn.
(1)an=n(2)存在整数λ=-1
(1)在已知式中,当n=1时,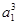 =
=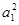 ,∵a1>0,∴a1=1,当n≥2时,
,∵a1>0,∴a1=1,当n≥2时,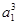 +
+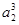 +
+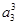 +…+
+…+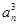 =
=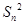 ,①
,①
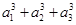 +…+
+…+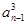 =
=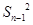 ,②
,②
①-②得,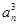 =
=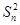 -
-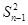 =(Sn-Sn-1)(Sn+Sn-1),
=(Sn-Sn-1)(Sn+Sn-1),
∵an>0,∴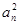 =Sn+Sn-1=2Sn-an,③
=Sn+Sn-1=2Sn-an,③
∵a1=1适合上式
当n≥2时,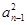 =2Sn-1-an-1,④
=2Sn-1-an-1,④
③-④得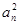 -
-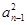 =2(Sn-Sn-1)-an+an-1=2an-an+an-1=an+an-1.
=2(Sn-Sn-1)-an+an-1=2an-an+an-1=an+an-1.
∵an+an-1>0,∴an-an-1=1,∴数列{an}是等差数列,首项为1,公差为1,可得an=n.
(2)由(1)知:bn=3n+(-1)n-1λ·2n
∴bn+1-bn=[3n+1+(-1)nλ·2n+1]-[3n+(-1)n-1λ·2n]=2·3n-3λ(-1)n-1·2n>0
∴(-1)n-1·λ<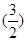 n-1,⑤
n-1,⑤
当n=2k-1,k=1,2,3,…时,⑤式即为λ<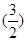 2k-2,⑥
2k-2,⑥
依题意,⑥式对k=1,2,3,…都成立,∴λ<1,
当n=2k,k=1,2,3,…时,⑤式即为λ>-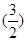 2k-1,⑦
2k-1,⑦
依题意,⑦式对k=1,2,3,…都成立,
∴λ>-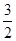 ,∴-
,∴-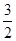 <λ<1,又λ≠0,∴存在整数λ=-1,使得对任意n∈N*,都有bn+1>bn.
<λ<1,又λ≠0,∴存在整数λ=-1,使得对任意n∈N*,都有bn+1>bn.
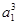 =
=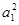 ,∵a1>0,∴a1=1,当n≥2时,
,∵a1>0,∴a1=1,当n≥2时,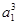 +
+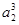 +
+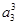 +…+
+…+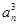 =
=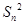 ,①
,①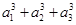 +…+
+…+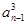 =
=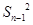 ,②
,②①-②得,
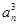 =
=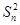 -
-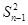 =(Sn-Sn-1)(Sn+Sn-1),
=(Sn-Sn-1)(Sn+Sn-1),∵an>0,∴
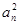 =Sn+Sn-1=2Sn-an,③
=Sn+Sn-1=2Sn-an,③∵a1=1适合上式
当n≥2时,
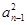 =2Sn-1-an-1,④
=2Sn-1-an-1,④③-④得
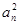 -
-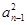 =2(Sn-Sn-1)-an+an-1=2an-an+an-1=an+an-1.
=2(Sn-Sn-1)-an+an-1=2an-an+an-1=an+an-1.∵an+an-1>0,∴an-an-1=1,∴数列{an}是等差数列,首项为1,公差为1,可得an=n.
(2)由(1)知:bn=3n+(-1)n-1λ·2n
∴bn+1-bn=[3n+1+(-1)nλ·2n+1]-[3n+(-1)n-1λ·2n]=2·3n-3λ(-1)n-1·2n>0
∴(-1)n-1·λ<
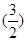 n-1,⑤
n-1,⑤当n=2k-1,k=1,2,3,…时,⑤式即为λ<
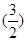 2k-2,⑥
2k-2,⑥依题意,⑥式对k=1,2,3,…都成立,∴λ<1,
当n=2k,k=1,2,3,…时,⑤式即为λ>-
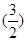 2k-1,⑦
2k-1,⑦依题意,⑦式对k=1,2,3,…都成立,
∴λ>-
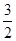 ,∴-
,∴-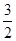 <λ<1,又λ≠0,∴存在整数λ=-1,使得对任意n∈N*,都有bn+1>bn.
<λ<1,又λ≠0,∴存在整数λ=-1,使得对任意n∈N*,都有bn+1>bn.
练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
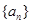 的前
的前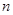 项和为
项和为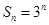 ,数列
,数列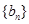 满足:
满足: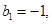
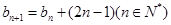 。
。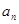 ;
;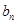 ;(3)若
;(3)若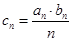 ,求数列
,求数列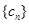 的前
的前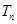 .
.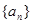 中,
中,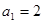 ,
,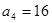 .
.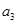 ,
,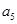 分别为等差数列
分别为等差数列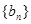 的第3项和第5项,试求数列
的第3项和第5项,试求数列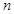 项和
项和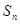 .
.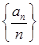 是递增数列;p4:数列{an+3nd}是递增数列.
是递增数列;p4:数列{an+3nd}是递增数列.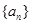 满足:当
满足:当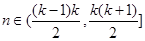 (
(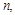
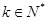 )时,
)时,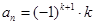 ,
,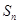 是数列
是数列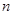 项和,定义集合
项和,定义集合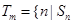 是
是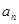 的整数倍,
的整数倍,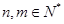 ,且
,且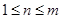
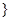 ,
,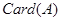 表示集合
表示集合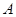 中元素的个数,则
中元素的个数,则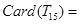 ,
,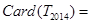 .
.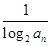 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得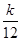 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.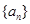 中,已知
中,已知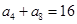 ,则该数列前11项的和
,则该数列前11项的和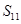 等于
等于