题目内容
已知y=f(x)是定义在R上的奇函数,且当x≥0时,f(x)=-
+
,则此函数的值域为______.
| 1 |
| 4x |
| 1 |
| 2x |
设t=
,当x≥0时,2x≥1,∴0<t≤1,
f(t)=-t2+t=-(t-
)2+
,
∴0≤f(t)≤
,
故当x≥0时,f(x)∈[0,
];
∵y=f(x)是定义在R上的奇函数,∴当x≤0时,f(x)∈[-
,0];
故函数的值域时[-
,
].
| 1 |
| 2x |
f(t)=-t2+t=-(t-
| 1 |
| 2 |
| 1 |
| 4 |
∴0≤f(t)≤
| 1 |
| 4 |
故当x≥0时,f(x)∈[0,
| 1 |
| 4 |
∵y=f(x)是定义在R上的奇函数,∴当x≤0时,f(x)∈[-
| 1 |
| 4 |
故函数的值域时[-
| 1 |
| 4 |
| 1 |
| 4 |

练习册系列答案
相关题目
 ,则( )
,则( )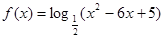 的单调递减区间是 .
的单调递减区间是 .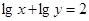 ,则
,则 +
+ 的最小值为( ).
的最小值为( ).


 .
.