题目内容
已知函数f（x）=a-
（x∈R），a为实数
（1）试用单调性定义证明对任意实数a，f（x）在其定义域上为增函数；
（2）试确定a的值，使f（x）为奇函数．
| 2 |
| 2x+1 |
（1）试用单调性定义证明对任意实数a，f（x）在其定义域上为增函数；
（2）试确定a的值，使f（x）为奇函数．
（1）设x1＜x2
∵f（x1）-f（x2）=-
+
=
，
由题设可得 2x1-2x2＜0，2x1+1＞0，2x2+1＞0，
∴f（x1）-f（x2）＜0，故函数在其定义域上为增函数．
（2）要使f（x）为奇函数，需f（0）=a-
=0，解得a=1．
经过检验，当a=1时，函数f（x）满足f（-x）=-f（x），f（x）为奇函数．
∵f（x1）-f（x2）=-
| 2 |
| 2x1+1 |
| 2 |
| 2x2+1 |
| 2(2x1-2x2) |
| (2x1+1)(2x2+1) |
由题设可得 2x1-2x2＜0，2x1+1＞0，2x2+1＞0，
∴f（x1）-f（x2）＜0，故函数在其定义域上为增函数．
（2）要使f（x）为奇函数，需f（0）=a-
| 2 |
| 1+1 |
经过检验，当a=1时，函数f（x）满足f（-x）=-f（x），f（x）为奇函数．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
（
且
）满足
，则
的解为（ ）
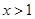
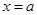是函数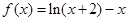
的极大值点，则
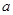等于（ ）
的结果是( )
