题目内容
已知tanα=2，tanβ=3，则tan（α+β）= ．
考点：两角和与差的正切函数
专题：三角函数的求值
分析：利用两角和的正切公式，即可求得答案．
解答：
解：∵tanα=2，tanβ=3，
∴tan（α+β）=
=
=-1．
故答案为：-1．
∴tan（α+β）=
| tanα+tanβ |
| 1-tanαtanβ |
| 2+3 |
| 1-2×3 |
故答案为：-1．
点评：本题考查两角和的正切，是基础题．
练习册系列答案
相关题目
数列{an}满足an+2an=2an+1（n∈N*），且a1=1，a2=2，则数列{an}的前2014项的乘积为（ ）
| A、22012 |
| B、22013 |
| C、22014 |
| D、22015 |
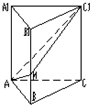如图，直三棱柱ABC-A1B1C1中，AB=1，BC=2，AC=