题目内容
【题目】(1)解不等式![]() ≥
≥![]() 的解集.
的解集.
(2) 关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1){x|x≤-3或x≥2};(2)![]() .
.
【解析】试题分析:(1)分段去绝对值求解不等式即可
(2)由于二次项系数含有参数,故需对其进行讨论.对于二次项系数不为0时,借助于相应二次函数的特征,可建立不等式组,从而求出实数m的取值范围.
试题解析:
(1)当x<-2时,不等式等价于-(x-1)-(x+2)≥5,解得x≤-3;
当-2≤x<1时,不等式等价于-(x-1)+(x+2)≥5,即3≥5,无解;
当x≥1时,不等式等价于x-1+x+2≥5,解得x≥2.
综上,不等式的解集为{x|x≤-3或x≥2}.
(2)①当![]() ,即
,即![]() 或
或![]() 时,要使原不等式的解集为R,则
时,要使原不等式的解集为R,则![]()
②当![]() 时,要使原不等式的解集为
时,要使原不等式的解集为![]() ,则有:
,则有:
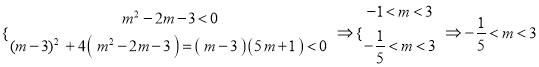
综合(1)(2)的![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 50 | 60 | 70 |
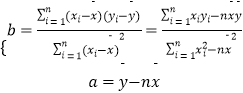
(1)画出散点图;
(2)求线性回归方程;
(3)预测当广告费支出为7百万元时的销售额.参考公式:.