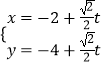题目内容
【题目】已知直线C1:  ( t 为参数),曲线C2:
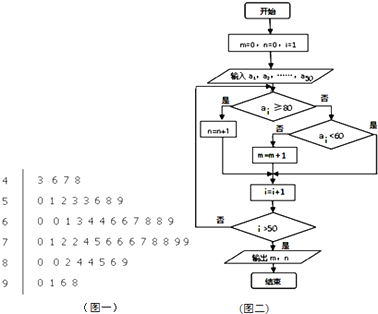
( t 为参数),曲线C2: ![]() (r>0,θ为参数).
(r>0,θ为参数).
(1)当r=1时,求C 1 与C2的交点坐标;
(2)点P 为曲线 C2上一动点,当r= ![]() 时,求点P 到直线C1距离最大时点P 的坐标.
时,求点P 到直线C1距离最大时点P 的坐标.
【答案】
(1)解:直线C1:  ( t 为参数)的普通方程为y=x﹣1,当r=1时,曲线C2:
( t 为参数)的普通方程为y=x﹣1,当r=1时,曲线C2: ![]() (r>0,θ为参数)的普通方程为x2+y2=1.
(r>0,θ为参数)的普通方程为x2+y2=1.
联立方程,可得C 1 与C2的交点坐标为(1,0),(0,﹣1);
(2)解:设P( ![]() ),则点P 到直线C1距离d=
),则点P 到直线C1距离d= ![]() =
= ![]()
当cos(θ+ ![]() )=﹣1,即θ=
)=﹣1,即θ= ![]() +2kπ(k∈Z)时,dmax=
+2kπ(k∈Z)时,dmax= ![]() ,此时P(﹣1,1).
,此时P(﹣1,1).
【解析】(1)参数方程化为普通方程,即可求C 1 与C2的交点坐标;(2)利用圆的参数方程,结合点到直线的距离公式、三角函数公式,即可求点P 到直线C1距离最大时点P 的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目