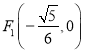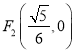题目内容
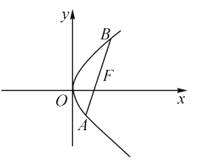
【题目】已知椭圆![]() 过点
过点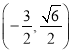 ,顺次连接椭圆的四个顶点得到的四边形的面积为
,顺次连接椭圆的四个顶点得到的四边形的面积为![]() ,点
,点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)已知点![]() ,是椭圆
,是椭圆![]() 上的两点.
上的两点.
(ⅰ)若![]() ,且
,且![]() 为等边三角形,求
为等边三角形,求![]() 的面积;
的面积;
(ⅱ)若![]() ,证明:
,证明: ![]() 不可能为等边三角形.
不可能为等边三角形.
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】试题分析:(Ⅰ)根据面积公式得到![]() ,以及点在曲线上,代入得到
,以及点在曲线上,代入得到![]() ,以及
,以及![]() ,求得
,求得![]() ;(Ⅱ)(ⅰ)根据等边三角形的性质,可得直线
;(Ⅱ)(ⅰ)根据等边三角形的性质,可得直线![]() 的倾斜角是
的倾斜角是![]() 或
或![]() ,这样求得直线
,这样求得直线![]() 的方程,联立椭圆方程,得到点
的方程,联立椭圆方程,得到点![]() 的坐标,求得面积;(ⅱ)因为
的坐标,求得面积;(ⅱ)因为![]() ,所以斜率存在,设直线
,所以斜率存在,设直线![]() 的方程是
的方程是![]() ,与椭圆方程联立,得到根与系数的关系,并且表示线段
,与椭圆方程联立,得到根与系数的关系,并且表示线段![]() 中点
中点![]() 的坐标,若是等边三角形,则
的坐标,若是等边三角形,则![]() ,可求得
,可求得![]() ,不合题意.
,不合题意.
试题解析:(Ⅰ)依题意, ![]() ,
, ![]() ,联立两式,解得
,联立两式,解得![]() ,
, ![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)(ⅰ)由![]() 且
且![]() 为等边三角形及椭圆的对称性可知,直线
为等边三角形及椭圆的对称性可知,直线![]() 和直线
和直线![]() 与
与![]() 轴的夹角为
轴的夹角为![]() ,由
,由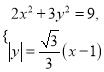 可得
可得![]() .
.
即![]() 或
或![]() ,当
,当![]() 时,
时, ![]() 的面积为
的面积为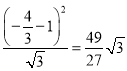 ;
;
当![]() 时,
时, ![]() 的面积为
的面积为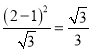 .
.
(ⅱ)因为![]() ,故直线
,故直线![]() 斜率存在,设直线
斜率存在,设直线![]() ,
, ![]() 中点为
中点为![]() ,联立
,联立![]() 消去
消去![]() 得,
得, ![]()
由![]() 得到
得到![]() ,①
,①
所以![]() ,
, ![]() ,
,
所以![]() .
.
又![]() ,若
,若![]() 为等边三角形,则有
为等边三角形,则有![]() ,
,
即![]() ,即
,即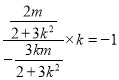 ,化简得
,化简得![]() ,②
,②
由②得点![]() 横坐标为
横坐标为![]() ,不合题意.
,不合题意.
故![]() 不可能为等边三角形.
不可能为等边三角形.
(用点差法求![]() 点坐标也可)
点坐标也可)

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目