题目内容
7.下列三个结论中正确的有①②(填序号).①函数f(x)=lg(x+1)+lg(x-1)的定义域是(1,+∞);
②若幂函数f(x)的图象经过点(2,4),则该函数为偶函数;
③函数y=5|x|的值域是(0,+∞).
分析 ①要使函数f(x)=lg(x+1)+lg(x-1)有意义,可得$\left\{\begin{array}{l}{x+1>0}\\{x-1>0}\end{array}\right.$,解得x,即可函数f(x)的定义域,进而判断出正误;
②设幂函数f(x)=xα(α为常数),由f(x)的图象经过点(2,4),代入解得α,可得f(x)=x2(x∈R),即可判断出函数的奇偶性;
③利用指数函数的单调性可得:函数y=5|x|≥50=1,可得其值域,进而判断出正误.
解答 解:①要使函数f(x)=lg(x+1)+lg(x-1)有意义,可得$\left\{\begin{array}{l}{x+1>0}\\{x-1>0}\end{array}\right.$,解得x>1.∴函数f(x)的定义域是(1,+∞),正确;
②设幂函数f(x)=xα(α为常数),由f(x)的图象经过点(2,4),∴4=2α,解得α=2,∴f(x)=x2(x∈R),则该函数为偶函数,正确;
③函数y=5|x|≥50=1,其值域是[1,+∞),因此不正确.
综上只有:①②正确.
故答案为:①②.
点评 本题考查了函数的定义域、奇偶性及其单调性、简易逻辑的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.在函数y=x2-1,y=x3,y=ex,y=lnx中,奇函数是( )
| A. | y=x2-1 | B. | y=x3 | C. | y=ex | D. | y=lnx |
2.cos(-30°)的值是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
12.已知几个命题:①若点P不在平面α内,A、B、C三点都在平面α内,则P、A、B、C四点不在同一平面内;②两两相交的三条直线在同一平面内;③两组对边分别相等的四边形是平行四边形.其中正确命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
19.设复数z1=1-i,z2=-1+xi(x∈R),若z1z2为纯虚数,则x的值是( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
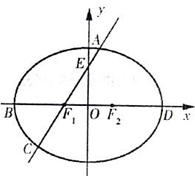 如图,在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{8}$=1(a>0)中,F1、F2分别为椭圆的左、右焦点,B、D分别为椭圆的左、右顶点,A为椭圆位于第一象限内的部分上的任意一点,直线AF1交椭圆于另一点C,交y轴于点E,且点F1、F2三等分线段BD.
如图,在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{8}$=1(a>0)中,F1、F2分别为椭圆的左、右焦点,B、D分别为椭圆的左、右顶点,A为椭圆位于第一象限内的部分上的任意一点,直线AF1交椭圆于另一点C,交y轴于点E,且点F1、F2三等分线段BD.