Question

17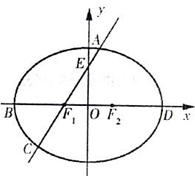．如图，在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{8}$=1（a＞0）中，F₁、F₂分别为椭圆的左、右焦点，B、D分别为椭圆的左、右顶点，A为椭圆位于第一象限内的部分上的任意一点，直线AF₁交椭圆于另一点C，交y轴于点E，且点F₁、F₂三等分线段BD．
（1）求a的值；
（2）若四边形EBCF₂为平行四边形，求点C的坐标；
（3）设λ=$\frac{S△A{F}_{1}O}{S△AEO}$，μ=$\frac{S△C{F}_{1}O}{S△CEO}$，求λ+μ的取值范围．

Answer 1

分析 （1）由点F₁、F₂三等分线段BD，可得2a=3×2c，利用e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-8}}{a}$=$\frac{1}{3}$，解得a．
（2）由（1）可得：B（-3，0），F₂（1，0）．设直线AF₁的方程为：y=k（x+1），则E（0，k）．（k＞0）．可得$\overrightarrow{E{F}_{2}}$=（1，-k），由于四边形EBCF₂为平行四边形，可得$\overrightarrow{BC}=\overrightarrow{E{F}_{2}}$，可得C坐标，代入椭圆方程即可解出．
（3）设直线AF₁的方程为：y=k（x+1），则E（0，k）．（2$\sqrt{2}＞$k＞0）．A（x₁，y₁），C（x₂，y₂）．λ=$\frac{S△A{F}_{1}O}{S△AEO}$=$\frac{|A{F}_{1}|}{|AE|}$，μ=$\frac{S△C{F}_{1}O}{S△CEO}$=$\frac{|C{F}_{1}|}{|CE|}$，可得λ+μ=$\frac{{x}_{1}}{{x}_{1}+1}$+$\frac{-1-{x}_{2}}{-{x}_{2}}$=$\frac{2{x}_{1}{x}_{2}+（{x}_{1}+{x}_{2}）+1}{{x}_{1}{x}_{2}+{x}_{2}}$，直线与椭圆方程联立化为（8+9k²）x²+18k²x+9k²-72=0．x₂=$\frac{-9{k}^{2}-24\sqrt{{k}^{2}+1}}{8+9{k}^{2}}$．利用根与系数的关系可得：λ+μ=$\frac{136-9{k}^{2}}{72+24\sqrt{{k}^{2}+1}}$，设$\sqrt{{k}^{2}+1}$=t∈（1，3）．则λ+μ=$\frac{145-9{t}^{2}}{72+24t}$=f（t），利用导数研究函数的单调性即可得出．

解答 解：（1）∵点F₁、F₂三等分线段BD，
∴2a=3×2c，解得e=$\frac{c}{a}$=$\frac{1}{3}$．
∴$\frac{\sqrt{{a}^{2}-8}}{a}$=$\frac{1}{3}$，解得a=3．
∴a=3．
（2）由（1）可得：B（-3，0），F₂（1，0）．
设直线AF₁的方程为：y=k（x+1），则E（0，k）．（k＞0）．
∴$\overrightarrow{E{F}_{2}}$=（1，-k），
∵四边形EBCF₂为平行四边形，
∴$\overrightarrow{BC}=\overrightarrow{E{F}_{2}}$，
∴$\overrightarrow{OC}=\overrightarrow{OB}$+$\overrightarrow{E{F}_{2}}$=（-2，-k），
把$\left\{\begin{array}{l}{x=-2}\\{y=-k}\end{array}\right.$代入椭圆方程可得：$\frac{4}{9}+\frac{{k}^{2}}{8}$=1，k＞0．
解得k=$\frac{2\sqrt{10}}{3}$．
∴C$（-2，-\frac{2\sqrt{10}}{3}）$．
（3）设直线AF₁的方程为：y=k（x+1），则E（0，k）．（2$\sqrt{2}＞$k＞0）．
A（x₁，y₁），C（x₂，y₂）．
λ=$\frac{S△A{F}_{1}O}{S△AEO}$=$\frac{|A{F}_{1}|}{|AE|}$，μ=$\frac{S△C{F}_{1}O}{S△CEO}$=$\frac{|C{F}_{1}|}{|CE|}$，
∴λ+μ=$\frac{|A{F}_{1}|}{|AE|}$+$\frac{|C{F}_{1}|}{|CE|}$=$\frac{{x}_{1}}{{x}_{1}+1}$+$\frac{-1-{x}_{2}}{-{x}_{2}}$=$\frac{2{x}_{1}{x}_{2}+（{x}_{1}+{x}_{2}）+1}{{x}_{1}{x}_{2}+{x}_{2}}$，
联立$\left\{\begin{array}{l}{y=k（x+1）}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1}\end{array}\right.$，化为（8+9k²）x²+18k²x+9k²-72=0．
∴△＞0，x₁+x₂=$\frac{-18{k}^{2}}{8+9{k}^{2}}$，${x}_{1}{x}_{2}=\frac{9{k}^{2}-72}{8+9{k}^{2}}$．
取x₂=$\frac{-9{k}^{2}-24\sqrt{{k}^{2}+1}}{8+9{k}^{2}}$．
∴λ+μ=$\frac{\frac{18{k}^{2}-144}{8+9{k}^{2}}-\frac{18{k}^{2}}{8+9{k}^{2}}+1}{\frac{9{k}^{2}-72}{8+9{k}^{2}}+\frac{-9{k}^{2}-24\sqrt{{k}^{2}+1}}{8+9{k}^{2}}}$=$\frac{136-9{k}^{2}}{72+24\sqrt{{k}^{2}+1}}$，
设$\sqrt{{k}^{2}+1}$=t∈（1，3）．
则λ+μ=$\frac{145-9{t}^{2}}{72+24t}$=f（t），
f′（t）=$\frac{-18t（72+24t）-24（145-9{t}^{2}）}{（72+24t）^{2}}$=$\frac{-（9{t}^{2}+54t+145）}{24（3+t）^{2}}$＜0，
∴函数f（t）在t∈（1，3）单调递减．
又f（1）=$\frac{17}{12}$，f（3）=$\frac{4}{9}$．
∴f（t）∈$（\frac{4}{9}，\frac{17}{12}）$．
∴λ+μ的取值范围是$（\frac{4}{9}，\frac{17}{12}）$．

点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、三角形面积计算公式、向量相等与平行四边形之间的关系，考查了推理能力与计算能力，属于难题．