题目内容
17．在函数y=x2-1，y=x3，y=ex，y=lnx中，奇函数是（ ）| A． | y=x2-1 | B． | y=x3 | C． | y=ex | D． | y=lnx |
分析 根据函数奇偶性的定义进行判断即可．
解答 解：设函数都为f（x），
则由y=x2-1，得f（-x）=x2-1=f（x），则函数f（x）偶函数．
由y=x3，得f（-x）=（-x）3=-x3=-f（x），则函数f（x）为奇函数，
y=ex，为增函数，为非奇非偶函数，
y=lnx的定义域为（0，+∞），关于原点不对称，为非奇非偶函数．
故选：B．
点评 本题主要考查函数奇偶性的判断，根据函数奇偶性的定义是解决本题的关键．
练习册系列答案
相关题目
7．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{3}，0≤x＜1}\\{f（x-1），x≥1}\end{array}\right.$，若g（x）=f（x）-kx-2k有5个不同的零点，则实数k的取值范围是（ ）
| A． | [$\frac{1}{7}$，$\frac{1}{6}$] | B． | [$\frac{1}{7}$，$\frac{1}{6}$） | C． | [$\frac{1}{8}$，$\frac{1}{7}$） | D． | （$\frac{1}{8}$，$\frac{1}{7}$] |
12．满足不等式y≤2及|x|≤y≤|x|+1所表示的平面区域的面积为（ ）
| A． | 2 | B． | 3 | C． | 6 | D． | 8 |
2．已知f （x）=x3+3ax2+3（a+2）x+1有极大值和极小值，则a的取值范围是（ ）
| A． | （-∞，-1）∪（2，+∞） | B． | （-2，1） | C． | （1，2） | D． | （-∞，-2）∪（1，+∞） |
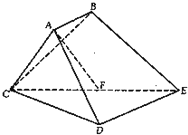已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2，AB=1，F为CE的中点．