Question

【题目】已知抛物线，过且斜率为1的直线与抛物线交于不同的两点

（1）求的取值范围；

（2）若线段的垂直平分线交轴于点，求面积的最大值。

Answer 1

【答案】（1）；（2）.

【解析】

（1）设出直线的方程，代入抛物线方程，化简后利用弦长公式求得的表达式，利用题目所给的范围求得的范围.（2）根据中点坐标公式求得中点的坐标.求得的值，写出三角形面积的表达式，结合（1）的结论可求得面积的最大值.

解：(1) 设直线与抛物线两交点的坐标分别为

直线的方程为,将代入抛物线方程,得 ,

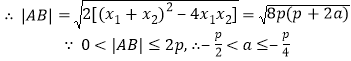
(2)设的垂直平分线交于点Q，令其坐标为则

,

所以|QM|2=(a+p-a)2+(p-0)2=2p2.又△MNQ为等腰直角三角形，所以|QM|=|QN|=，

所以

即△NAB面积的最大值为。