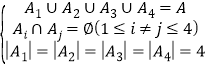题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,直线l与椭圆C交于A、B两点,且
,直线l与椭圆C交于A、B两点,且![]()
(1)求椭圆C的方程;
(2)若A、B两点关于原点O的对称点分别为![]() ,且
,且![]() ,判断四边形
,判断四边形![]() 是否存在内切的定圆?若存在,请求出该内切圆的方程;若不存在,请说明理由.
是否存在内切的定圆?若存在,请求出该内切圆的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]()
【解析】
(1)因为![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,解得
,解得![]() ,代入方程即可 (2)①当直线
,代入方程即可 (2)①当直线![]() 的斜率
的斜率![]() 存在时,设
存在时,设![]() ,由
,由 ,
,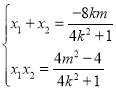 ,因为
,因为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,原点
,原点![]() 到直线
到直线![]() 的距离
的距离![]() ,同理可证,原点
,同理可证,原点![]() 到达
到达![]() 的距离都为
的距离都为![]() ,四边形
,四边形![]() 存在内切的定圆,且该定圆的方程为
存在内切的定圆,且该定圆的方程为![]() ②当直线
②当直线![]() 的斜率不存在时,同理说明即可
的斜率不存在时,同理说明即可
解:(1)因为![]() ,所以
,所以![]() ,.因为直线
,.因为直线![]() 与椭圆
与椭圆![]() 交于,两点,且
交于,两点,且![]() ,所以
,所以![]() ,所以
,所以![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
所以椭圆的方程为![]()
(2)①当直线![]() 的斜率
的斜率![]() 存在时,设
存在时,设![]() 由
由
得![]() ,
,![]() ,
,
所以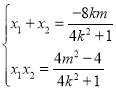 ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,即
,即![]() 所以
所以![]() ,所以原点
,所以原点![]() 到直线
到直线![]() 的距离
的距离![]()
根据椭圆的对称性,同理可证,原点![]() 到达
到达![]() 的距离都为
的距离都为![]() ,
,
所以四边形![]() 存在内切的定圆,且该定圆的方程为
存在内切的定圆,且该定圆的方程为![]()
②当直线![]() 的斜率不存在时,设直线
的斜率不存在时,设直线![]() 的方程为
的方程为![]() ,不妨设
,不妨设![]() 分别为直线
分别为直线![]() 与椭圆
与椭圆![]() 的上、下交点,则
的上、下交点,则![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,解得
,解得![]() ,
,
所以此时原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
根据椭圆的对称性,同理可证,原点![]() 到达
到达![]() 的距离都为
的距离都为![]() ,
,
所以四边形![]() 存在内切的定圆,且该定圆的方程为
存在内切的定圆,且该定圆的方程为![]() .
.
综上可知,四边形![]() 存在内切的定圆,且该定圆的方程为
存在内切的定圆,且该定圆的方程为![]()

【题目】BMI指数(身体质量指数,英文为Body Mass Index,简称BMI)是衡量人体胖瘦程度的一个标准,BMI=体重(kg)/身高(m)的平方. 根据中国肥胖问题工作组标准,当BMI![]() 时为肥胖. 某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,得到被调查者的频率分布直方图如图:
时为肥胖. 某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,得到被调查者的频率分布直方图如图:

(1)求被调查者中肥胖人群的BMI 平均值![]() ;
;
(2)根据频率分布直方图,完成下面的![]() 列联表,并判断能有多大(百分数)的把握认为 35 岁以上成人高血压与肥胖有关?
列联表,并判断能有多大(百分数)的把握认为 35 岁以上成人高血压与肥胖有关?
肥胖 | 不肥胖 | 总计 | |
高血压 | |||
非高血压 | |||
总计 |
参考公式: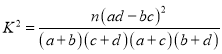 ,其中
,其中![]() .
.
参考数据:
| 0.25 | 0.10 | 0.050 | 0.010 | 0.001 |
| 1.323 | 2.706 | 3.841 | 6.635 | 10.828 |