题目内容
已知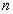 为正整数,试比较
为正整数,试比较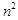 与
与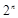 的大小 .
的大小 .
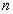 为正整数,试比较
为正整数,试比较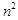 与
与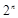 的大小 .
的大小 .当n=1时,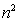 <
<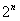 ;当n=2时,
;当n=2时,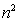 =
=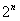 ; 当n=3时,
; 当n=3时,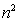 >
>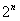 ; 当n=4时,
; 当n=4时,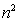 =
=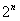 ;,当
;,当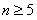 时,
时,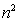 <
<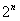
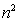 <
<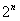 ;当n=2时,
;当n=2时,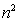 =
=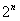 ; 当n=3时,
; 当n=3时,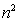 >
>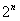 ; 当n=4时,
; 当n=4时,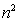 =
=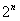 ;,当
;,当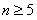 时,
时,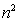 <
<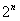
试题分析:解:当n=1时,
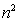 <
<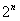 ; 1分
; 1分当n=2时,
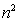 =
=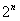 ; 2分
; 2分当n=3时,
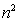 >
>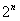 ; 3分
; 3分当n=4时,
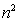 =
=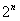 ; 4分
; 4分当n=5时,
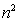 <
<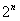 ; 当n=6时,
; 当n=6时,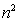 <
<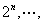
猜想:当
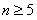 时,
时,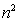 <
<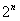 5分
5分下面下面用数学归纳法证明:
(1)当n=5时,由上面的探求可知猜想成立 6分
(2)假设n=k(
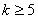 )时猜想成立,即
)时猜想成立,即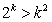 7分
7分则
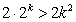 ,
, 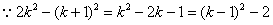 ,
,当
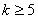 时
时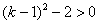
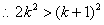 ,从而
,从而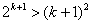
所以当n=k+1时,猜想也成立 9分
综合(1)(2),对
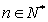 猜想都成立 10分
猜想都成立 10分点评:对于不等式的证明可以通过通过对于n的讨论来得到,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
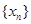 对一切
对一切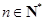 均满足
均满足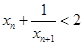 .证明:
.证明: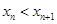 ;
;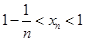 .
.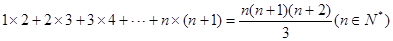 .
.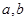 ,使等式
,使等式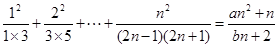 对于一切
对于一切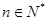 都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
都成立?若不存在,说明理由;若存在,请用数学归纳法证明?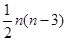 条时,第一步检验n等于( )
条时,第一步检验n等于( )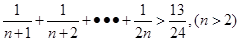 ”的过程中,由n=k到n=k+1时,不等式的左边( )
”的过程中,由n=k到n=k+1时,不等式的左边( )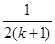

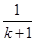
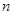 的函数
的函数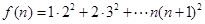
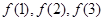 ;
;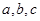 使得
使得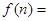
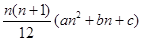 对一切自然数
对一切自然数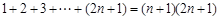 时,当
时,当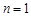 时左边表达式是 ;从
时左边表达式是 ;从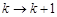 需增添的项的是 。
需增添的项的是 。