题目内容
设关于正整数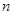 的函数
的函数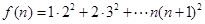
(1)求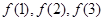 ;
;
(2)是否存在常数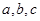 使得
使得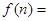
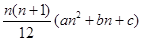 对一切自然数
对一切自然数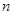 都成立?并证明你的结论
都成立?并证明你的结论
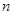 的函数
的函数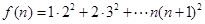
(1)求
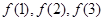 ;
;(2)是否存在常数
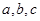 使得
使得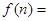
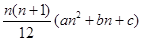 对一切自然数
对一切自然数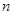 都成立?并证明你的结论
都成立?并证明你的结论(1)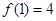 ,
,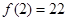 ,
,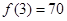
(2)根据数学归纳法思想,先利用特殊值来得到参数的a,b,c的值,然后对于解题的结果运用数学归纳法加以证明。
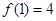 ,
,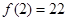 ,
,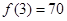
(2)根据数学归纳法思想,先利用特殊值来得到参数的a,b,c的值,然后对于解题的结果运用数学归纳法加以证明。
试题分析:解:(1)
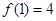 ,
,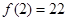 ,
,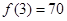 3分
3分(2)假设存在a,b,c使题设的等式成立,这时,n=1,2,3得
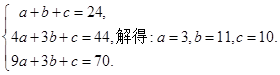 6分
6分于是,对n=1,2,3下面等式成立:
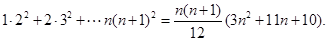 8分
8分记

假设n=k时上式成立,即
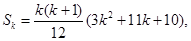 10分
10分那么
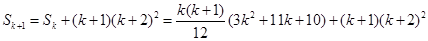
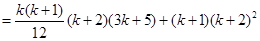
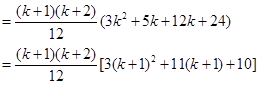
也就是说,等式对n=k+1也成立 3分
综上所述,当a=3,b=11,c=10时,题设的等式对一切自然数n成立 14分
点评:主要是考查了运用数学归纳法证明与自然数相关的命题,以及归纳猜想思想的运用。属于中档题。

练习册系列答案
相关题目
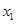 ,
,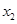 是函数
是函数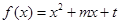 的两个零点,其中常数
的两个零点,其中常数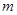 ,
,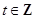 ,设
,设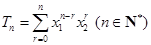 .
.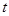 表示
表示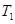 ,
,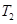 ;
;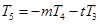 ;
;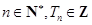 .
.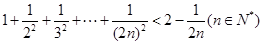 ,第二步证明“从
,第二步证明“从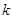 到
到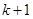 ”,左端增加的项数是( )
”,左端增加的项数是( )



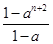 (n∈N*,a≠1),在验证n=1时,左边所得的项为( )
(n∈N*,a≠1),在验证n=1时,左边所得的项为( )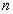 为正整数,试比较
为正整数,试比较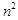 与
与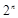 的大小 .
的大小 .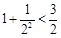 ,
,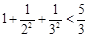 ,
,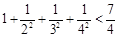 ,
,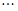 则可归纳出式子( )
则可归纳出式子( )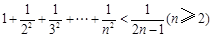
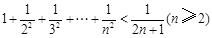
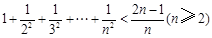
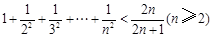
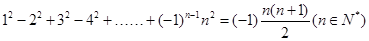 ”,
”,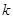 步到第
步到第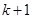 步时,左边应加上 .
步时,左边应加上 .