题目内容
是否存在常数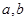 ,使等式
,使等式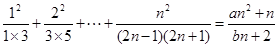 对于一切
对于一切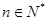 都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
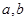 ,使等式
,使等式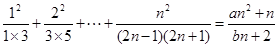 对于一切
对于一切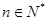 都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
都成立?若不存在,说明理由;若存在,请用数学归纳法证明?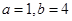 ,见解析.
,见解析.本试题考查了抽象函数式的运用。若存在常数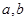 使等式成立,则将
使等式成立,则将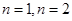 代入上式可以得到a,b,的关系式,
代入上式可以得到a,b,的关系式,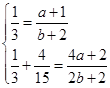 得
得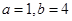 ,即有
,即有
然后证明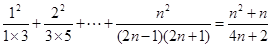 对于一切
对于一切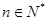 成立,运用数学归纳法可得。
成立,运用数学归纳法可得。
解:若存在常数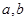 使等式成立,则将
使等式成立,则将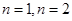 代入上式,有
代入上式,有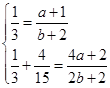
得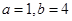 ,即有
,即有
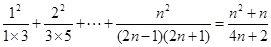 对于一切
对于一切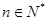 成立………4分
成立………4分
证明如下:
(1)当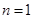 时,左边=
时,左边=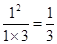 ,右边=
,右边=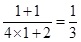 ,所以等式成立 …………6分
,所以等式成立 …………6分
(2)假设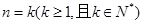 时等式成立,即
时等式成立,即
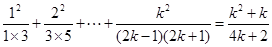
当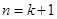 时,
时,
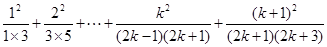 =
=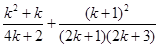
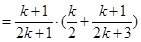 =
=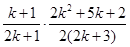 =
=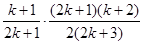
=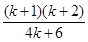 =
=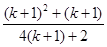
也就是说,当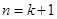 时,等式成立, …………11分
时,等式成立, …………11分
综上所述,可知等式对任何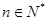 都成立。 …………12分
都成立。 …………12分
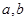 使等式成立,则将
使等式成立,则将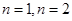 代入上式可以得到a,b,的关系式,
代入上式可以得到a,b,的关系式,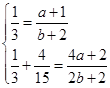 得
得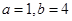 ,即有
,即有然后证明
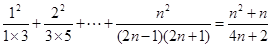 对于一切
对于一切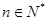 成立,运用数学归纳法可得。
成立,运用数学归纳法可得。解:若存在常数
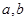 使等式成立,则将
使等式成立,则将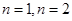 代入上式,有
代入上式,有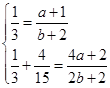
得
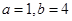 ,即有
,即有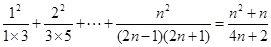 对于一切
对于一切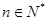 成立………4分
成立………4分证明如下:
(1)当
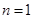 时,左边=
时,左边=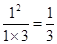 ,右边=
,右边=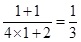 ,所以等式成立 …………6分
,所以等式成立 …………6分(2)假设
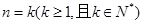 时等式成立,即
时等式成立,即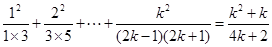
当
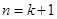 时,
时,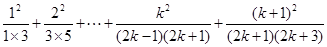 =
=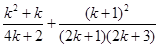
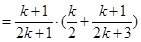 =
=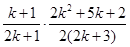 =
=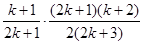
=
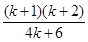 =
=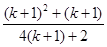
也就是说,当
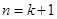 时,等式成立, …………11分
时,等式成立, …………11分综上所述,可知等式对任何
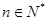 都成立。 …………12分
都成立。 …………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
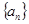 满足
满足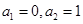 ,且对于任意的正整数
,且对于任意的正整数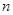 都有
都有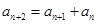 成立.
成立.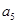 ;(2)证明:存在大于1的正整数
;(2)证明:存在大于1的正整数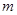 ,使得对于任意的正整数
,使得对于任意的正整数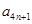 都能被
都能被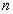 为正整数,试比较
为正整数,试比较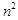 与
与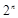 的大小 .
的大小 .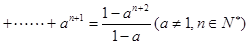 在验证n=1成立时,左边计算所得结果为 ( )
在验证n=1成立时,左边计算所得结果为 ( )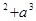
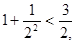 ,
,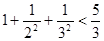 ,
, ……可归纳出式子为( )。
……可归纳出式子为( )。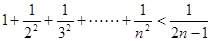
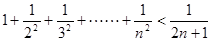
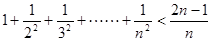
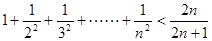
 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且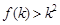 成立时,总可推出
成立时,总可推出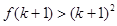 成立”. 那么,下列命题总成立的是( )
成立”. 那么,下列命题总成立的是( )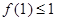 成立,则
成立,则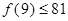 成立;
成立;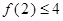 成立,则
成立,则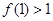 成立;
成立;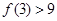 成立,则当
成立,则当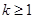 时,均有
时,均有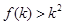 成立;
成立;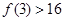 成立,则当
成立,则当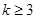 时,均有
时,均有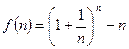 ,其中
,其中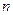 为正整数.
为正整数.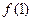 ,
,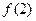 ,
,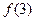 的值;
的值;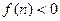 的正整数
的正整数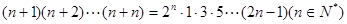 ”时,从
”时,从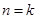 到
到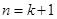 ,等式的左边需要增乘的代数式是__________ ;
,等式的左边需要增乘的代数式是__________ ;