题目内容
各项均为正数的数列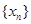 对一切
对一切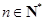 均满足
均满足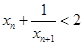 .证明:
.证明:
(1)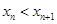 ;
;
(2)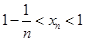 .
.
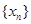 对一切
对一切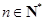 均满足
均满足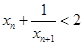 .证明:
.证明:(1)
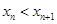 ;
;(2)
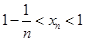 .
.(1)详见解析,(2)详见解析.
试题分析:(1)作差证明不等式,因为
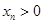 ,
,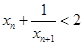 ,所以
,所以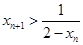 ,且
,且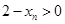 .
.因此
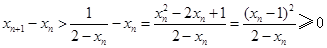 .即
.即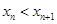 .(2)本题证明:
.(2)本题证明: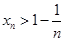 用数学归纳法,而证明
用数学归纳法,而证明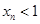 用反证法. ① 当
用反证法. ① 当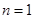 时,由题设
时,由题设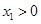 可知
可知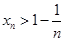 成立;② 假设
成立;② 假设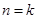 时,
时,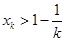 ,
,当
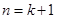 时,由(1)得,
时,由(1)得,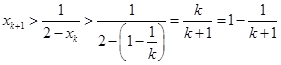 .由①,②可得,
.由①,②可得,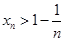 .假设存在自然数
.假设存在自然数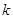 ,使得
,使得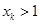 ,则一定存在自然数
,则一定存在自然数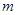 ,使得
,使得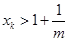 .因为
.因为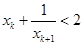 ,
,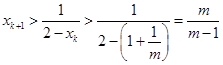 ,
,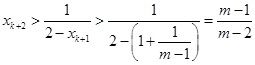 , ,
, ,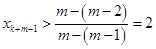 ,与题设
,与题设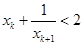 矛盾,所以,
矛盾,所以,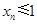 .若
.若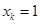 ,则
,则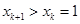 ,根据上述证明可知存在矛盾.
,根据上述证明可知存在矛盾.【证明】(1)因为
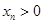 ,
,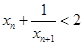 ,与题设
,与题设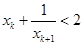 矛盾,所以,
矛盾,所以,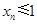 .若
.若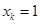 ,则
,则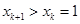 ,根据上述证明可知存在矛盾.
,根据上述证明可知存在矛盾.所以
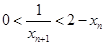 ,
,所以
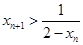 ,且
,且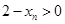 .
.因为
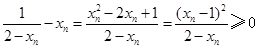 .
.所以
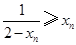 ,
,所以
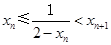 ,即
,即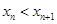 . 4分
. 4分(注:用反证法证明参照给分)
(2)下面用数学归纳法证明:
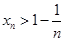 .
.① 当
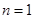 时,由题设
时,由题设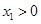 可知结论成立;
可知结论成立;② 假设
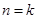 时,
时,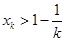 ,
,当
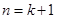 时,由(1)得,
时,由(1)得,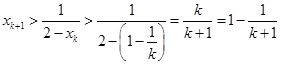 .
.由①,②可得,
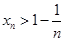 . 7分
. 7分下面先证明
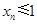 .
.假设存在自然数
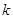 ,使得
,使得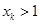 ,则一定存在自然数
,则一定存在自然数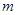 ,使得
,使得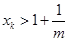 .
.因为
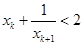 ,
,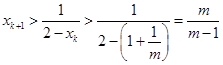 ,
,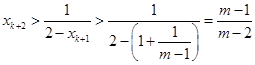 , ,
, ,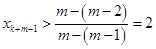 ,
,与题设
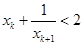 矛盾,所以,
矛盾,所以,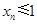 .
. 若
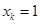 ,则
,则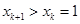 ,根据上述证明可知存在矛盾.
,根据上述证明可知存在矛盾.所以
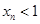 成立. 10分
成立. 10分
练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
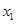 ,
,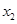 是函数
是函数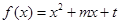 的两个零点,其中常数
的两个零点,其中常数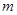 ,
,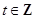 ,设
,设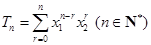 .
.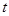 表示
表示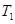 ,
,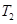 ;
;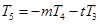 ;
;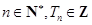 .
.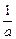 )(b+
)(b+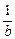 )≥
)≥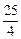 .
.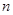 条直线,其中任何两条不平行,任何三条不共点,当
条直线,其中任何两条不平行,任何三条不共点,当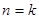 时把平面分成的区域数记为
时把平面分成的区域数记为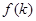 ,则
,则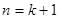 时
时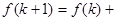 .
.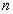 为正整数,试比较
为正整数,试比较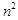 与
与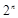 的大小 .
的大小 .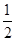 +
+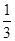 +…+
+…+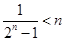 (
(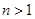 ,
,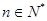 ),在验证
),在验证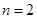 成立时,左式是____.
成立时,左式是____.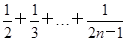 <n,其中n>1且n∈N*,在验证n=2时,式子的左边等于________.
<n,其中n>1且n∈N*,在验证n=2时,式子的左边等于________.