Question

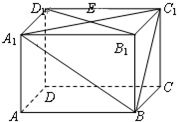如图，在长方体ABCD-A₁B₁C₁D₁中，底面ABCD是边长为2的正方形，AA₁=1，E是A₁C₁与B₁D₁的交点．
（1）作出面A₁BC₁与面ABCD的交线l，并写出作法；
（2）若以D为坐标原点，分别以DA，DC，DD₁所在的直线为x轴、y轴、z 轴，建立空间直角坐标系，试写出B，E两点的坐标，并求BE的长；
（3）求BC₁与面BDD₁B₁所成角的正切值．

Answer 1

分析：（1）在面ABCD内过点B作AC的平行线BE，（或过点B作A₁C₁的平行线），得到此平行线即为所求作的交线l．
（2）根据条件中所给的坐标系，写出两个点的坐标，利用两点之间的距离公式写出两点之间的距离．
（3）要求线面角，包括三个过程，一作二证三求，通过垂直做出面的垂直线，得到线面角，在直角三角形中利用三角函数的定义做出正切值．

解答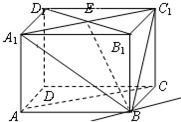：解：（1）在面ABCD内过点B作AC的平行线BE，（或过点B作A₁C₁的平行线）
则此平行线即为所求作的交线l
（2）B（2，2，0），E（1，1，1）
BE=

3

（3）连接BE，
∵C₁E⊥B₁D₁，C₁E⊥BB₁
∴C₁E⊥面BDD₁B₁，
∴∠C₁BE为BC₁与面BDD₁B₁所成的角，
又∵C₁E=

2

，BE=

3

∴tan∠C₁BE=

C1E

BE

=

2

3

=

6

3

点评：本题考查直线乙平面所成的角和两点之间的距离，解决本题的关键是看出与平面垂直的线，得到线面角．