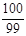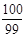题目内容
设等差数列的前n项和为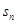 ,
,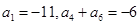 ,则当
,则当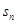 取最小值时的n值为
取最小值时的n值为
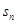 ,
,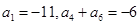 ,则当
,则当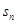 取最小值时的n值为
取最小值时的n值为| A. 6 | B. 7 | C. 8 | D. 9 |
A
条件已提供了首项,故用“a1,d”法,再转化为关于n的二次函数解得.
解:设该数列的公差为d,则a4+a6=2a1+8d=2×(-11)+8d=-6,解得d=2,
所以Sn=-11n+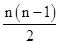 ×2=n2-12n=(n-6)2-36,所以当n=6时,Sn取最小值.
×2=n2-12n=(n-6)2-36,所以当n=6时,Sn取最小值.
故选A
解:设该数列的公差为d,则a4+a6=2a1+8d=2×(-11)+8d=-6,解得d=2,
所以Sn=-11n+
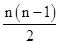 ×2=n2-12n=(n-6)2-36,所以当n=6时,Sn取最小值.
×2=n2-12n=(n-6)2-36,所以当n=6时,Sn取最小值.故选A

练习册系列答案
相关题目
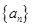 满足
满足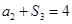 ,
,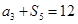 ,则
,则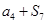 的值是( )
的值是( )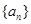 的公比
的公比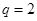 ,前
,前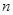 项和为
项和为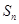 ,则
,则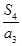 的值为
的值为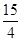
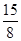
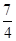
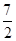
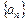 中,
中,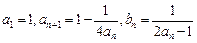 ,其中
,其中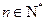 .
.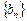 为等差数列;
为等差数列;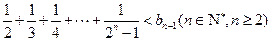
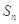 是等差数列
是等差数列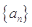 的前n项和,有
的前n项和,有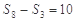 ,则
,则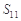 的值为( )
的值为( )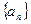 满足:
满足: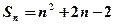 ,其中
,其中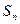 为数列
为数列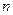 项和.
项和.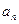 ;
;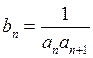 ,求
,求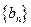 的前n项和Tn..
的前n项和Tn..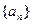 的前n项和为
的前n项和为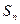 ,并且满足
,并且满足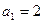 ,
,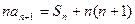 ,
,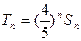 ,问是否存在正整数
,问是否存在正整数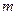 ,对一切正整数
,对一切正整数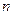 ,总有
,总有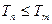 ,若存在,求
,若存在,求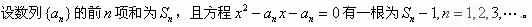
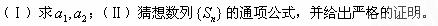
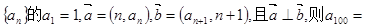 ( )
( )