题目内容
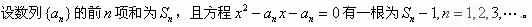
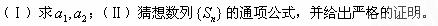
解:(Ⅰ)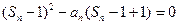 即
即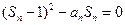
令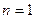
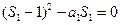 解得
解得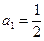
令
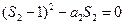 解得
解得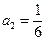
(Ⅱ)解法一:
化简得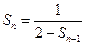
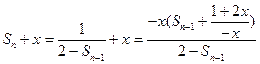
令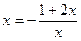 解得
解得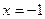
所以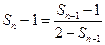
令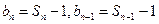
所以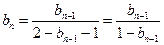 化简
化简 得
得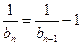
而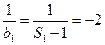
所以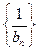 是以-2为首项,-1为公差的等差数列
是以-2为首项,-1为公差的等差数列
所以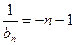 得
得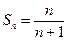
解法二:猜想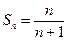 ,下面用数学归纳法证明:
,下面用数学归纳法证明:
(1) 当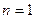 时,
时,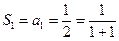 ,所以当
,所以当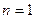 时猜想成立
时猜想成立
(2) 假设当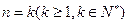 时,猜想成立
时,猜想成立
即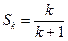
那么当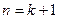 时,
时,

所以当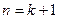 时猜想成立。
时猜想成立。
综合(1)、(2)可得对于任意的正整数猜想都成立。
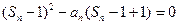 即
即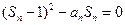
令
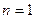
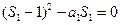 解得
解得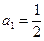
令

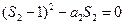 解得
解得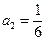
(Ⅱ)解法一:

化简得
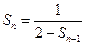
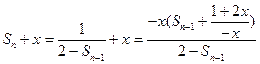
令
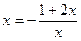 解得
解得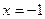
所以
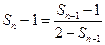
令
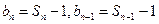
所以
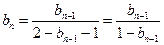 化简
化简 得
得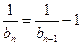
而
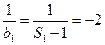
所以
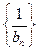 是以-2为首项,-1为公差的等差数列
是以-2为首项,-1为公差的等差数列所以
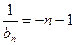 得
得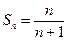
解法二:猜想
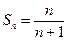 ,下面用数学归纳法证明:
,下面用数学归纳法证明:(1) 当
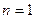 时,
时,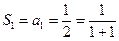 ,所以当
,所以当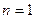 时猜想成立
时猜想成立(2) 假设当
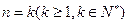 时,猜想成立
时,猜想成立即
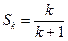
那么当
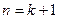 时,
时,
所以当
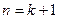 时猜想成立。
时猜想成立。综合(1)、(2)可得对于任意的正整数猜想都成立。
略

练习册系列答案
相关题目
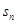 ,
,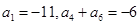 ,则当
,则当 中,
中,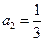 ,公比
,公比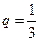 。
。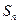 为
为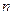 项和,证明:
项和,证明: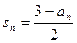
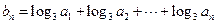 ,求数列
,求数列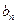 的通项公式.
的通项公式. 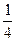 (an+1)
(an+1)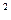 (n∈N*).
(n∈N*).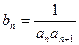 ,记数列{bn}的前n项和为
,记数列{bn}的前n项和为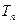 ,求
,求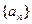 是等差数列,其前n项和为
是等差数列,其前n项和为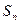 ,已知
,已知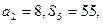
 式; (2)设
式; (2)设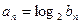 ,证明
,证明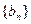 是等比数列,并求其前n项和
是等比数列,并求其前n项和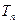 。
。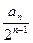 }的前n项和。
}的前n项和。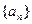 中,已知
中,已知
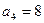 ,求:
,求: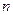 项和
项和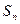 .
.
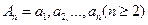 满足
满足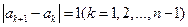 ,数列
,数列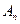 为
为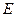 数列,记
数列,记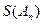 =
=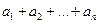 .
.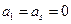 ,且
,且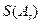 〉0的
〉0的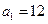 ,n=2000,证明:E数列
,n=2000,证明:E数列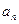 =2011;
=2011;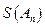 =0?如果存在,写出一个满足条件的E数列
=0?如果存在,写出一个满足条件的E数列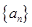 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且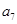 是
是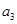 与
与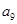 的等比中项,
的等比中项,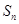 为
为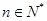 ,则
,则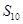 的值为
的值为