题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() .
.
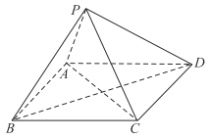
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设![]() 与
与![]() 交点为
交点为![]() ,连接
,连接![]() ,可知点
,可知点![]() 为
为![]() 的中点,利用等腰三角形三线合一的性质可得出
的中点,利用等腰三角形三线合一的性质可得出![]() ,由菱形的性质可得出
,由菱形的性质可得出![]() ,利用线面垂直的判定定理可得出
,利用线面垂直的判定定理可得出![]() 平面
平面![]() ,再利用面面垂直的判定定理可得出平面
,再利用面面垂直的判定定理可得出平面![]() 平面
平面![]() ;
;
(2)设![]() ,可求得
,可求得![]() ,
,![]() ,利用勾股定理可求得
,利用勾股定理可求得![]() ,然后以点
,然后以点![]() 为坐标原点,
为坐标原点,![]() 方向为
方向为![]() 轴正方向,
轴正方向,![]() 方向为
方向为![]() 轴正方向建立空间直角坐标系,求出平面
轴正方向建立空间直角坐标系,求出平面![]() 的一个法向量,利用空间向量法可求得直线
的一个法向量,利用空间向量法可求得直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)记![]() 与
与![]() 交点为
交点为![]() ,连接
,连接![]() ,
,
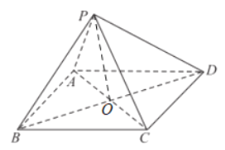
![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,
又![]() 四边形
四边形![]() 为菱形,
为菱形,![]() .
.
![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以,平面
,所以,平面![]() 平面
平面![]() ;
;
(2)设![]() ,
,![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() .
.
因为![]() ,所以在
,所以在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
即![]() ,解得
,解得![]() ,
,![]() ,
,
由(1)知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
以![]() 为原点,
为原点,![]() 方向为
方向为![]() 轴正方向,
轴正方向,![]() 方向为
方向为![]() 轴正方向,建立如图空间直角坐标系.则
轴正方向,建立如图空间直角坐标系.则![]() 、
、![]() 、
、![]() 、
、 ,.,
,.,
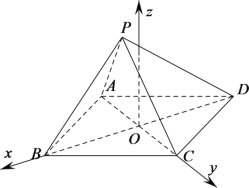
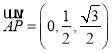 ,
,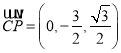 ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由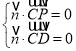 ,则
,则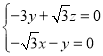 ,
,
令![]() ,解得
,解得![]() ,
,![]() ,即
,即![]() ,
,
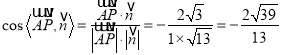 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】如表提供了工厂技术改造后某种型号设备的使用年限![]() 和所支出的维修费
和所支出的维修费![]() (万元)的几组对照数据:
(万元)的几组对照数据:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式: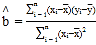 ,
,![]() .
.
(1)若知道![]() 对
对![]() 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?
