题目内容
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
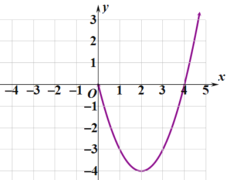
时,![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴右侧的图象,如图所示.
轴右侧的图象,如图所示.
(1)画出函数![]() 在
在![]() 轴左侧的图象,根据图象写出函数
轴左侧的图象,根据图象写出函数![]() 在
在![]() 上的单调区间;
上的单调区间;
(2)求函数![]() 在
在![]() 上的解析式;
上的解析式;
(3)解不等式![]() .
.
【答案】(1)图见解析;函数的单调增区间是![]() ,单调减区间是
,单调减区间是![]() (2)
(2)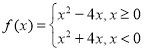 (3)
(3)![]()
【解析】
(1)根据偶函数的对称性作出函数图象,由函数图象读出函数的单调区间;
(2)当![]() 时,
时,![]() ,再根据当
,再根据当![]() 时,
时,![]() ,可得
,可得![]() .再根据函数
.再根据函数![]() 为偶函数,可得
为偶函数,可得![]() ,由此能求出函数
,由此能求出函数![]() 的解析式.
的解析式.
(3)因为![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;由函数图象读出解集即可;
;由函数图象读出解集即可;
解:(1)如图作函数图象.
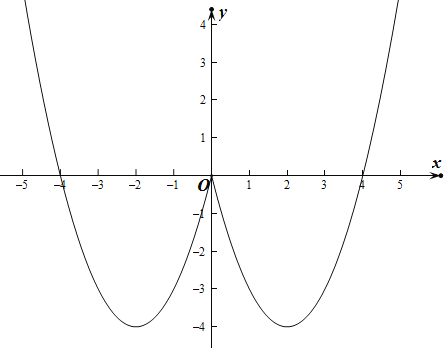
函数的单调增区间是:![]() ,单调减区间是:
,单调减区间是:![]() .
.
(2)因为![]() 时,
时,![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
又因为![]() 是定义在
是定义在![]() 上的偶函数,
上的偶函数,
所以,当![]() 时,
时,![]() .
.
综上: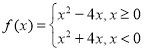 .
.
(3)因为![]()
当![]() 时,
时,![]() ,即
,即![]() ;当
;当![]() 时,
时,![]() ,即
,即![]() ;
;
所以解集为:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】如表提供了工厂技术改造后某种型号设备的使用年限![]() 和所支出的维修费
和所支出的维修费![]() (万元)的几组对照数据:
(万元)的几组对照数据:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式: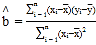 ,
,![]() .
.
(1)若知道![]() 对
对![]() 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?
【题目】越接近高考学生焦虑程度越强,四个高三学生中大约有一个有焦虑症,经有关机构调查,得出距离高考周数与焦虑程度对应的正常值变化情况如下表:
周数x | 6 | 5 | 4 | 3 | 2 | 1 |
正常值y | 55 | 63 | 72 | 80 | 90 | 99 |
(1)作出散点图:

(2)根据上表数据用最小二乘法求出y关于x的线性回归方程 (精确到0.01);
(3)根据经验,观测值为正常值的0.85~1.06为正常,若1.06~1.12为轻度焦虑,1.12~1.20为中度焦虑,1.20及其以上为重度焦虑,若为中度焦虑及其以上,则要进行心理疏导,若一个学生在距高考第二周时观测值为100,则该学生是否需要进行心理疏导?
(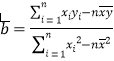 ,
, ![]() )
)