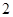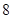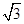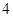题目内容
已知点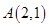 在抛物线
在抛物线 上,直线
上,直线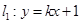 (
(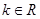 ,且
,且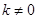 )与抛物线
)与抛物线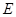 ,相交于
,相交于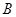 、
、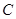 两点,直线
两点,直线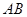 、
、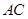 分别交直线
分别交直线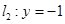 于点
于点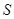 、
、 .
.
(1)求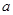 的值;
的值;
(2)若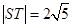 ,求直线
,求直线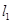 的方程;
的方程;
(3)试判断以线段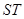 为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
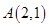 在抛物线
在抛物线 上,直线
上,直线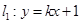 (
(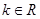 ,且
,且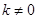 )与抛物线
)与抛物线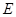 ,相交于
,相交于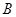 、
、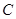 两点,直线
两点,直线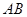 、
、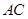 分别交直线
分别交直线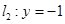 于点
于点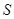 、
、 .
.(1)求
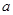 的值;
的值;(2)若
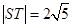 ,求直线
,求直线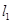 的方程;
的方程;(3)试判断以线段
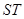 为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.(1)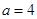 ;(2)
;(2)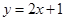 或
或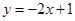 ;(3)存在,且两个定点坐标为
;(3)存在,且两个定点坐标为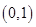 和
和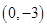 .
.
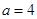 ;(2)
;(2)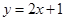 或
或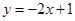 ;(3)存在,且两个定点坐标为
;(3)存在,且两个定点坐标为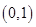 和
和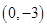 .
.试题分析:(1)将点
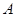 代入抛物线的方程即可求出
代入抛物线的方程即可求出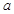 的值;(2)解法1是先设点
的值;(2)解法1是先设点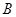 、
、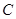 的坐标分别为
的坐标分别为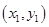 、
、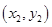 ,将直线
,将直线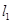 的方程与抛物线
的方程与抛物线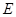 的方程联立求出
的方程联立求出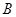 、
、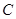 的坐标,并求出
的坐标,并求出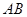 、
、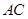 的直线方程,与直线
的直线方程,与直线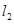 的方程联立求出
的方程联立求出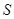 、
、 的坐标,利用两点间的距离公式列等式求出
的坐标,利用两点间的距离公式列等式求出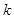 的值,从而求出直线
的值,从而求出直线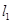 的方程;解法2是设直线
的方程;解法2是设直线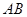 的方程为
的方程为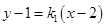 ,点
,点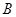 的坐标为
的坐标为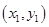 ,分别将直线
,分别将直线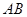 的方程与抛物线和直线
的方程与抛物线和直线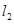 的方程求出点
的方程求出点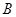 、
、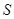 的坐标,然后设直线
的坐标,然后设直线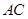 的方程为
的方程为 ,利用同样的方法求出点
,利用同样的方法求出点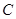 、
、 的坐标,利用点
的坐标,利用点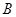 、
、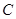 都在直线
都在直线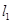 上,结合两点连线的斜率等于
上,结合两点连线的斜率等于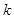 值以及点
值以及点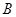 在直线
在直线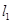 得到
得到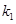 、
、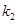 与
与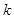 之间的等量关系,然后再利用两点间的距离公式列等式求出
之间的等量关系,然后再利用两点间的距离公式列等式求出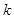 的值,从而求出直线
的值,从而求出直线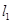 的方程;(3)解法1是求出线段
的方程;(3)解法1是求出线段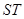 的中点的坐标,然后写出以
的中点的坐标,然后写出以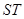 为直径的圆的方程,结合韦达定理进行化简,根据方程的结构特点求出定点的坐标;解法2是设
为直径的圆的方程,结合韦达定理进行化简,根据方程的结构特点求出定点的坐标;解法2是设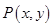 为以
为以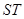 为直径的圆上的一点,由
为直径的圆上的一点,由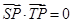 得到以
得到以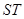 为直径的圆的方程,然后圆的方程的结构特点求出定点的坐标.
为直径的圆的方程,然后圆的方程的结构特点求出定点的坐标.试题解析:(1)
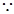 点
点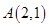 在抛物线
在抛物线 上,
上,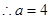 .
.第(2)、(3)问提供以下两种解法:
解法1:(2)由(1)得抛物线
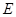 的方程为
的方程为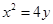 .
.设点
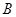 、
、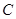 的坐标分别为
的坐标分别为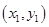 、
、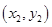 ,依题意,
,依题意,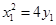 ,
,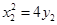 ,
,由
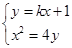 消去
消去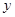 得
得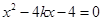 ,
,解得
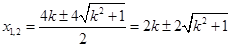 .
.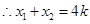 ,
,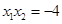 ,
,直线
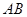 的斜率
的斜率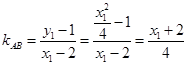 ,
,故直线
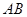 的方程为
的方程为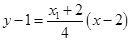 .
.令
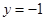 ,得
,得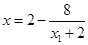 ,
,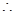 点
点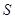 的坐标为
的坐标为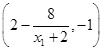 .
.同理可得点
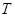 的坐标为
的坐标为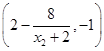 .
.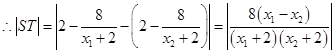
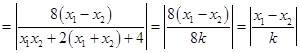 .
.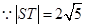 ,
,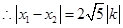 .
.由
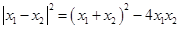 ,得
,得 ,
,解得
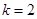 ,或
,或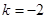 ,
,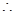 直线
直线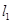 的方程为
的方程为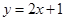 ,或
,或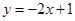 .
.(3)设线段
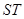 的中点坐标为
的中点坐标为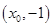 ,
,则
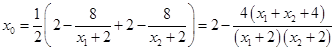
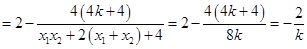 .
.而
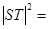
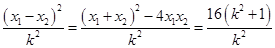 ,
,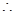 以线段
以线段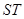 为直径的圆的方程为
为直径的圆的方程为
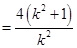 .
.展开得
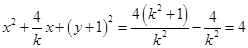 .
.令
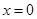 ,得
,得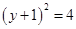 ,解得
,解得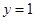 或
或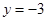 .
.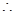 以线段
以线段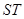 为直径的圆恒过两个定点
为直径的圆恒过两个定点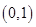 、
、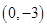 .
.解法2:(2)由(1)得抛物线
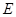 的方程为
的方程为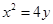 .
.设直线
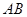 的方程为
的方程为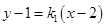 ,点
,点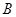 的坐标为
的坐标为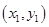 ,
,由
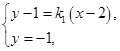 解得
解得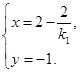
 点
点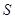 的坐标为
的坐标为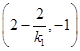 .
.由
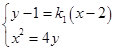 ,消去
,消去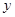 ,得
,得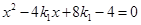 ,
,即
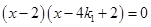 ,解得
,解得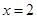 或
或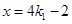 .
.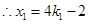 ,
,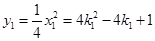 .
.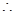 点
点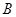 的坐标为
的坐标为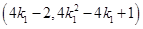 .
.同理,设直线
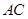 的方程为
的方程为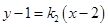 ,
,则点
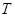 的坐标为
的坐标为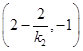 ,点
,点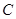 的坐标为
的坐标为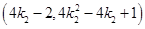 .
.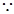 点
点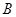 、
、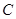 在直线
在直线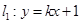 上,
上,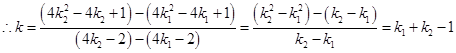 .
.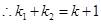 . 5分
. 5分又
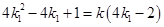
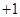 ,得
,得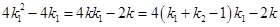 ,
,化简得
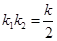 .
.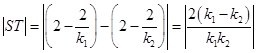 ,
,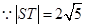 ,
,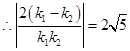 .
.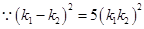 .
.由
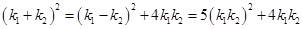 ,
,得
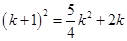 ,
,解得
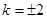 .
.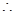 直线
直线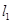 的方程为
的方程为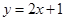 ,或
,或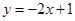 .
.(3)设点
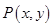 是以线段
是以线段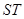 为直径的圆上任意一点,
为直径的圆上任意一点,则
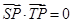 ,
,得
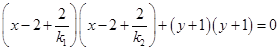 ,
,整理得,
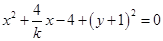 .
.令
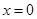 ,得
,得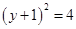 ,解得
,解得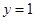 或
或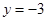 .
.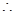 以线段
以线段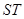 为直径的圆恒过两个定点
为直径的圆恒过两个定点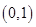 、
、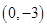 .
.
练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
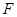
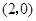 与分别在
与分别在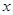 轴、
轴、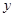 轴上的动点
轴上的动点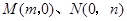 满足:
满足: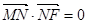 ,动点
,动点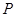 满足
满足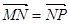 .
.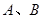 两点,直线
两点,直线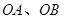 与直线
与直线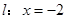 分别交于点
分别交于点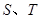 (
(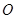 为坐标原点);
为坐标原点);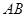 为直径的圆的位置关系;
为直径的圆的位置关系;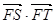 是否为定值?并证明你的结论.
是否为定值?并证明你的结论.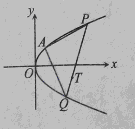
 ,求点A的坐标;
,求点A的坐标;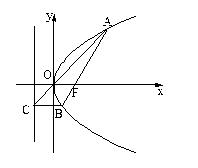
 的焦点作直线交抛物线于
的焦点作直线交抛物线于 两点,线段
两点,线段 的中点
的中点 的纵坐标为2,则线段
的纵坐标为2,则线段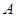 在抛物线
在抛物线 上,且点
上,且点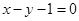 的距离为
的距离为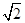 ,则点
,则点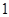
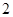
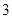
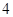
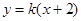 (k>0)与抛物线
(k>0)与抛物线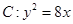 相交于A、B两点,
相交于A、B两点,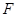 为
为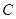 的焦点,若
的焦点,若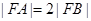 ,则k的值为()
,则k的值为()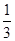
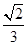
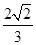
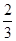
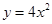 的焦点到准线的距离是( )
的焦点到准线的距离是( )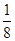
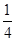
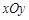 中,抛物线
中,抛物线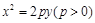 上纵坐标为
上纵坐标为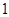 的点到焦点的距离
的点到焦点的距离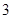 ,则焦点到准线的距离为( )
,则焦点到准线的距离为( )