题目内容
(12分)有一块边长为4的正方形钢板,现对其切割、焊接成一个长方体无盖容器(切、焊损耗忽略不计)。有人应用数学知识作如下设计:在钢板的四个角处各切去一个全等的小正方形,剩余部分围成一个长方体,该长方体的高是小正方形的边长。
(1)请你求出这种切割、焊接而成的长方体容器的最大容积 ;
;
(2)请你判断上述方案是否是最佳方案,若不是,请设计一种新方案,使材料浪费最少,且所得长方体容器的容积 。
。
(1)请你求出这种切割、焊接而成的长方体容器的最大容积
 ;
;(2)请你判断上述方案是否是最佳方案,若不是,请设计一种新方案,使材料浪费最少,且所得长方体容器的容积
 。
。(1)当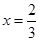 时,
时, 取最大值
取最大值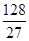 ;
;
(2)重新设计方案如下:
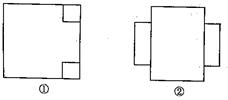
如图①,在正方形的两个角处各切下一个边长为1的小正方形;如图②,将切下的小正方形焊在未切口的正方形一边的中间;将图②焊成长方体容器.新焊长方体容器底面是一长方形,长为3,宽为2,此长方体容积为6,故第二种方案符合要求.
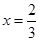 时,
时, 取最大值
取最大值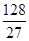 ;
;(2)重新设计方案如下:

如图①,在正方形的两个角处各切下一个边长为1的小正方形;如图②,将切下的小正方形焊在未切口的正方形一边的中间;将图②焊成长方体容器.新焊长方体容器底面是一长方形,长为3,宽为2,此长方体容积为6,故第二种方案符合要求.
本试题主要是考查了导数在研究函数中的运用。求解最值问题。
(1)因为设切去正方形边长为x,则焊接成的长方体的底面边长为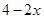 ,高为x,
,高为x,
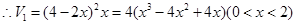 ,然后求解导数来判定单调性得到极值,进而求解最值。
,然后求解导数来判定单调性得到极值,进而求解最值。
(2)在正方形的两个角处各切下一个边长为1的小正方形;如图②,将切下的小正方形焊在未切口的正方形一边的中间;将图②焊成长方体容器.新焊长方体容器底面是一长方形,长为3,宽为2,此长方体容积为6,故第二种方案符合要求
(1)设切去正方形边长为x,则焊接成的长方体的底面边长为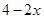 ,高为x,
,高为x,
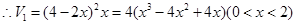 ……(2分)
……(2分)
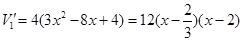 . ……(3分)
. ……(3分)
当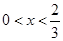 时,
时,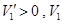 是关于x的增函数;
是关于x的增函数;
当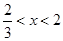 时,
时,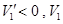 是关于x的减函数.
是关于x的减函数.
∴当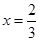 时,
时, 取最大值
取最大值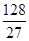 ……(7分)
……(7分)
(2)重新设计方案如下:

如图①,在正方形的两个角处各切下一个边长为1的小正方形;如图②,将切下的小正方形焊在未切口的正方形一边的中间;将图②焊成长方体容器.新焊长方体容器底面是一长方形,长为3,宽为2,此长方体容积为6,故第二种方案符合要求.……(12分)
(1)因为设切去正方形边长为x,则焊接成的长方体的底面边长为
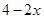 ,高为x,
,高为x,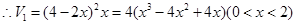 ,然后求解导数来判定单调性得到极值,进而求解最值。
,然后求解导数来判定单调性得到极值,进而求解最值。(2)在正方形的两个角处各切下一个边长为1的小正方形;如图②,将切下的小正方形焊在未切口的正方形一边的中间;将图②焊成长方体容器.新焊长方体容器底面是一长方形,长为3,宽为2,此长方体容积为6,故第二种方案符合要求
(1)设切去正方形边长为x,则焊接成的长方体的底面边长为
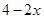 ,高为x,
,高为x,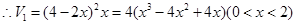 ……(2分)
……(2分)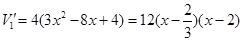 . ……(3分)
. ……(3分)当
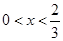 时,
时,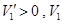 是关于x的增函数;
是关于x的增函数;当
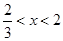 时,
时,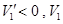 是关于x的减函数.
是关于x的减函数.∴当
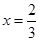 时,
时, 取最大值
取最大值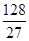 ……(7分)
……(7分)(2)重新设计方案如下:

如图①,在正方形的两个角处各切下一个边长为1的小正方形;如图②,将切下的小正方形焊在未切口的正方形一边的中间;将图②焊成长方体容器.新焊长方体容器底面是一长方形,长为3,宽为2,此长方体容积为6,故第二种方案符合要求.……(12分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象的横坐标伸长为原来的3倍,纵坐标缩短为原来的
的图象的横坐标伸长为原来的3倍,纵坐标缩短为原来的 ,则所得函数的解析式为( )
,则所得函数的解析式为( )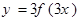





 的图象如图所示,则导函数
的图象如图所示,则导函数 的图象可能是( )
的图象可能是( )
 ,若x=-1为函数
,若x=-1为函数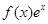 的一个极值点,则下列图象不可能为
的一个极值点,则下列图象不可能为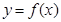 的图象是( )
的图象是( )
 ),EF在移动过程中扫过平行四边形OABC的面积为
),EF在移动过程中扫过平行四边形OABC的面积为 (图中阴影部分),
(图中阴影部分), 的图象大致是( ).
的图象大致是( ).
 与
与 (
(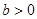 且
且 )的图象可能是( )
)的图象可能是( )
 <0在x∈(0,
<0在x∈(0,  )时恒成立,则m的取值范围是_______
)时恒成立,则m的取值范围是_______  的图像如下图,那么导函数
的图像如下图,那么导函数 的图像可能是( )
的图像可能是( )
