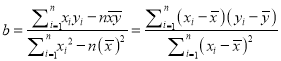题目内容
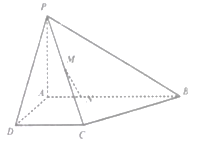
【题目】如图所示,四棱锥![]() 中,四边形
中,四边形![]() 是直角梯形,
是直角梯形, ![]() 底面
底面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 点在
点在![]() 上,且
上,且![]() .
.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)见解析;(II)![]() ,
,
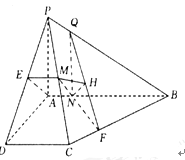
【解析】试题分析:(1)要证MN∥平面PAD,只需在面PAD内找到一条直线和MN平行即可,而根据条件,易作辅助线过M作ME∥CD交PD于E,连接AE,下证MN∥AE;
(2)求直线MN与平面PCB所成的角,关键找直线MN在平面PCB内的射影,而根据条件,易作辅助线过N点作NQ∥AP交BP于点Q,NF⊥CB交CB于点F,连接QF,过N点作NH⊥QF交QF于H,连接MH,下证NH⊥平面PBC,∴∠NMH为直线MN与平面PCB所成的角.解△MNH即可.
试题解析:
(1)过点![]() 作
作![]() 交
交![]() 于
于![]() 点,连结
点,连结![]() ,
,
![]() , 又
, 又![]()
![]() 为平行四边形,
为平行四边形, ![]() 平面
平面![]() .
.
(2)过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,
连结![]() ,过
,过![]() 点作
点作![]() 于
于![]() ,连结
,连结![]()
易知![]() 面
面![]() 而
而![]() 面
面![]() ,
,![]()
而![]() 面
面![]() ,
, ![]() 为直线
为直线![]() 与平面
与平面![]() 所成角,
所成角,
![]() 通过计算可得
通过计算可得![]() ,
,
 ,
,
![]() ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.

练习册系列答案
相关题目
【题目】某工厂为了对新研发的一种产品进行合理定价,将该定价按事先拟定的价格进行试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?
附:  .
.