题目内容
已知点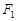 、
、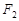 为双曲线
为双曲线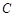 :
: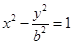
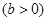 的左、右焦点,过
的左、右焦点,过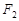 作垂直于
作垂直于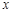 轴的直线,在
轴的直线,在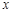 轴上方交双曲线
轴上方交双曲线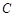 于点
于点 ,且
,且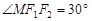 ,圆
,圆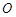 的方程是
的方程是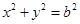 .
.
(1)求双曲线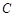 的方程;
的方程;
(2)过双曲线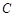 上任意一点
上任意一点 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为 、
、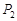 ,求
,求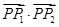 的值;
的值;
(3)过圆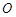 上任意一点
上任意一点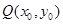 作圆
作圆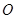 的切线
的切线 交双曲线
交双曲线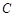 于
于 、
、 两点,
两点,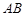 中点为
中点为 ,求证:
,求证: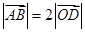 .
.
(1)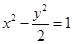 ;(2)
;(2)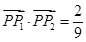 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)作出解题所需图形,对照图形和双曲线的定义不难解决此问题;(2)按照数量积的定义即需求模和夹角,这都可以通过解析几何的工具性知识在形式上得到表示,然后通过设而不求和整体思想得以解决;(3)通过分析可将等式的证明转化为垂直关系的判定,仍然运用设而不求和整体思想来解决,注意要对直线的斜率是否存在分情况讨论,这样解题才严谨.
试题解析:(1)设 、
、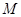 的坐标分别为
的坐标分别为 、
、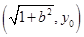
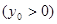
因为点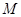 在双曲线
在双曲线 上,所以
上,所以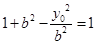 ,即
,即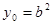 ,所以
,所以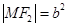
在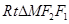 中,
中,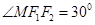 ,
,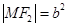 ,所以
,所以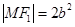 2分
2分
由双曲线的定义可知: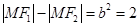
故双曲线 的方程为:
的方程为: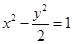 4分
4分
(2)由条件可知:两条渐近线分别为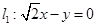 ,
, 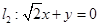 5分
5分
设双曲线 上的点
上的点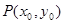 ,设
,设 的倾斜角为
的倾斜角为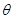 ,则
,则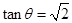
则点 到两条渐近线的距离分别为
到两条渐近线的距离分别为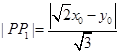 ,
,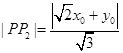 7分
7分
因为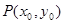 在双曲线
在双曲线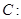
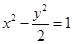 上,所以
上,所以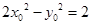
又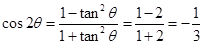 ,从而
,从而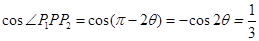
所以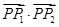
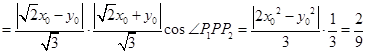 10分
10分
(3)由题意,即证: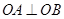 .
.
设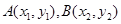 ,切线
,切线 的方程为:
的方程为: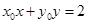 ,且
,且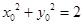 11分
11分
①当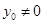 时,将切线
时,将切线 的方程代入双曲线
的方程代入双曲线 中,化简得:
中,化简得: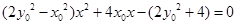
所以: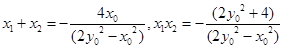
又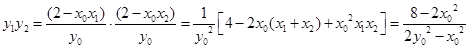 13分
13分
所以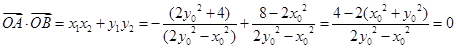 15分
15分
②当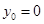 时,易知上述结论也成立. 所以
时,易知上述结论也成立. 所以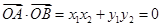 &n
&n

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
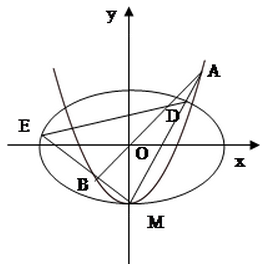
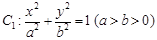 的离心率为
的离心率为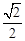 ,
,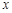 轴被曲线
轴被曲线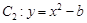 截得的线段长等于
截得的线段长等于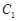 的短轴长.
的短轴长.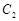 与
与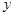 轴的交点为
轴的交点为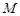 ,过坐标原点
,过坐标原点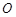 的直线
的直线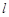 与
与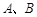 ,直线
,直线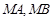 分别与
分别与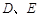 .
.
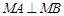 ;
;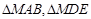 的面积分别为
的面积分别为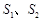 ,若
,若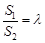 ,求
,求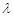 的取值范围.
的取值范围. 曲线的一个焦点,并与
曲线的一个焦点,并与 ,求抛物线的方程和双曲线的方程.
,求抛物线的方程和双曲线的方程. 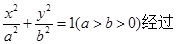 点
点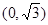 ,离心率为
,离心率为 ,左右焦点分别为
,左右焦点分别为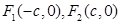
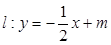 与椭圆交于
与椭圆交于 两点,与以
两点,与以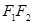 为直径的圆交于
为直径的圆交于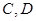 两点,且满足
两点,且满足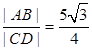 ,求直线
,求直线 的方程.
的方程.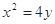 ,过点
,过点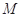
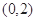 作直线与抛物线交于两点
作直线与抛物线交于两点 ,
,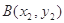 ,过
,过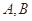 分别作抛物线的切线,两切线的交点为
分别作抛物线的切线,两切线的交点为 .
.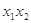 的值;
的值;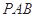 面积的最小值.
面积的最小值.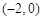 ,
,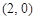 ,并且经过点
,并且经过点 ,求它的标准方程.
,求它的标准方程.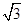 ,且其三个顶点均在抛物线E:x2=2py(p>0)上.
,且其三个顶点均在抛物线E:x2=2py(p>0)上.
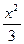 -
-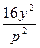 =1的左焦点在抛物线y2=2px的准线上,则p的值为______
=1的左焦点在抛物线y2=2px的准线上,则p的值为______