题目内容
叙述并证明两个平面垂直的判定定理。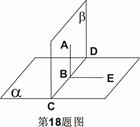

见解析.
本试题主要考查了两个平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,
那么这两个平面互相垂直。并且通过作辅助线,利用定义法证明二面角的平面角的大小为90度即可。首先作出二面角,然后利用三角形求解,从而得到证明。
解:两个平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,
那么这两个平面互相垂直。……….4分,
证明:设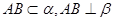 ,
,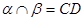 ,……….6分,
,……….6分,
则由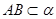 知AB、CD共面,
知AB、CD共面,
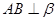 ,
,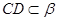 ,
,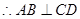 ,垂足为点B,……….8分,
,垂足为点B,……….8分,
在平面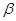 内过点B作直线
内过点B作直线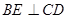 ,
,
则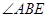 是二面角
是二面角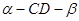 的平面角,……….10分,
的平面角,……….10分,
又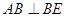 ,即二面角
,即二面角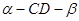 是直二面角,
是直二面角,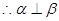 ………….12分
………….12分
那么这两个平面互相垂直。并且通过作辅助线,利用定义法证明二面角的平面角的大小为90度即可。首先作出二面角,然后利用三角形求解,从而得到证明。
解:两个平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,
那么这两个平面互相垂直。……….4分,
证明:设
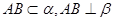 ,
,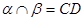 ,……….6分,
,……….6分,则由
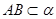 知AB、CD共面,
知AB、CD共面,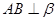 ,
,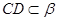 ,
,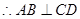 ,垂足为点B,……….8分,
,垂足为点B,……….8分,在平面
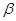 内过点B作直线
内过点B作直线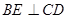 ,
,则
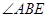 是二面角
是二面角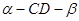 的平面角,……….10分,
的平面角,……….10分,又
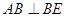 ,即二面角
,即二面角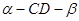 是直二面角,
是直二面角,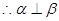 ………….12分
………….12分
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
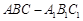 中,
中,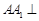 平面
平面 ,
,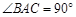 ,
,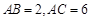 , 点
, 点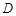 在线段
在线段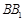 上,且
上,且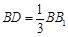 ,
,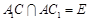 .
.
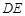 与平面
与平面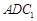 与平面
与平面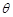 ,若
,若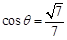 ,求
,求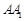 的长;
的长;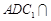 平面
平面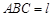 ,求直线
,求直线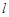 与
与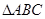 中,若
中,若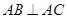 ,
,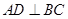 于
于 ,则
,则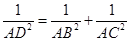 .在四面体
.在四面体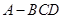 中,若
中,若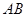 ,
,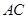 ,
,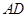 两两垂直,
两两垂直,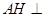 底面
底面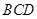 ,垂足为
,垂足为 ,则类似的结论是什么?并说明理由.
,则类似的结论是什么?并说明理由.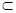 平面α,直线c
平面α,直线c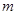 ,
,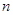 为两条不同的直线,
为两条不同的直线,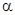 ,
,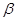 为两个不同的平面,则下列命题是真命题的是( )
为两个不同的平面,则下列命题是真命题的是( )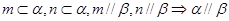
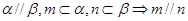
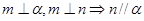
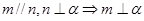
 为两条不同的直线,
为两条不同的直线,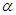 、
、 为两个不同的平面,则下列命题正确的是
为两个不同的平面,则下列命题正确的是 ;
;


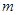 、
、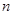 为不同的两条直线),
为不同的两条直线),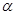 、
、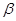 为不同的两个平面)
为不同的两个平面)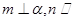
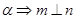
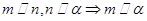
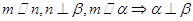
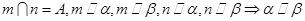
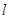 ,
,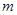 是两条不同的直线,
是两条不同的直线,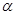 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( ) ,
, ,则
,则
 ,则
,则
 ,
, ,则
,则