题目内容
13.在三角形ABC中,∠A、∠B、∠C的对边分别为a、b、c,且$\frac{cosC}{cosB}$=$\frac{2sinA-sinC}{sinB}$.(1)求∠B的大小;
(2)若b=$\sqrt{7}$,a+c=4,求三角形ABC的面积.
分析 (1)先根据正弦定理用正弦表示出边,然后代入到已知条件中,再由两角和与差的公式整理可得到cosB的值,最后可得角B的值.
(2)根据余弦定理将b=$\sqrt{7}$,a+c=4代入求出ac的值,再由三角形的面积公式可求得结果.
解答 解:(1)∵$\frac{cosC}{cosB}$=$\frac{2sinA-sinC}{sinB}$,
∴sinBcosC=2sinAcosB-sinCcosB,
∴sinBcosC+sinCcosB=2sinAcosB,
∴sin(B+C)=2sinAcosB,
∴sinA=2sinAcosB,
∴2cosB=1
∴cosB=$\frac{1}{2}$,
∴B=60°;
(2)∵b2=a2+c2-2accos60°=(a+c)2-2ac-2ac•cosB
∴将b=$\sqrt{7}$,a+c=4,代入整理得ac=3
故三角形ABC的面积S=$\frac{1}{2}acsinB$=$\frac{3\sqrt{3}}{4}$.
点评 本题主要考查正弦定理和余弦定理的应用,在求值时经常用到边和角的相互转化,这里一般是用正弦定理.

练习册系列答案
相关题目
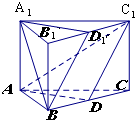 如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,求证:l1∥l2.
如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,求证:l1∥l2.