题目内容
2.已知集合A={1,2,3,4,5,6,7},一一映射f:A→A满足:对任意的x∈A,均有f[f(f(x))]=x,则这样的映射f的个数为351.分析 根据已知中一一映射f:A→A满足:对任意的x∈A,均有f[f(f(x))]=x,集合A={1,2,3,4,5,6,7},分类讨论满足条件的映射的个数,综合讨论结果,可得答案.
解答 解:①若f(a)=a,
则对任意的x∈A,均有f[f(f(x))]=x,
则这样的映射f的个数为1个,
②如果从集合A抽取三个元素a,b,c满足:f(a)=b,f(b)=c,f(c)=a,
再从剩下的四个元素抽取三个元素,d,e,f满足:f(d)=e,f(e)=f,f(f)=d,
剩下的元素满足:f(g)=g,
则对任意的x∈A,均有f[f(f(x))]=x,
则这样的映射f的个数为${C}_{7}^{3}{C}_{4}^{3}÷{A}_{2}^{2}$=70个,
③如果从集合A抽取三个元素a,b,c满足:f(a)=c,f(b)=a,f(c)=b,
再从剩下的四个元素抽取三个元素,d,e,f满足:f(d)=f,f(e)=d,f(f)=e,
剩下的元素满足:f(g)=g,
则对任意的x∈A,均有f[f(f(x))]=x,
则这样的映射f的个数为${C}_{7}^{3}{C}_{4}^{3}÷{A}_{2}^{2}$=70个,
④如果从集合A抽取三个元素a,b,c满足:f(a)=b,f(b)=c,f(c)=a,
再从剩下的四个元素抽取三个元素,d,e,f满足:f(d)=f,f(e)=d,f(f)=e,
剩下的元素满足:f(g)=g,
则对任意的x∈A,均有f[f(f(x))]=x,
则这样的映射f的个数为${C}_{7}^{3}{C}_{4}^{3}$=140个,
⑤如果从集合A抽取三个元素a,b,c满足:f(a)=b,f(b)=c,f(c)=a,
再从剩下的四个元素d,e,f,g满足:f(d)=d,f(e)=e,f(f)=f,f(g)=g,
则对任意的x∈A,均有f[f(f(x))]=x,
则这样的映射f的个数为${C}_{7}^{3}$=35个,
⑥如果从集合A抽取三个元素a,b,c满足:f(a)=c,f(b)=a,f(c)=b,
再从剩下的四个元素d,e,f,g满足:f(d)=d,f(e)=e,f(f)=f,f(g)=g,
则对任意的x∈A,均有f[f(f(x))]=x,
则这样的映射f的个数为${C}_{7}^{3}$=35个,
综上这样的映射共有1+70+70+140+35+35=351个,
故答案为:351
点评 本题考查的知识点是映射,分类讨论思想,本题分类标准比较麻烦,容易漏分,难度中档.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案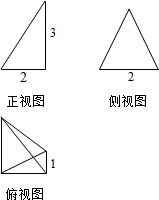 一个几何体的三视图如图所示,则该几何体的体积为( )
一个几何体的三视图如图所示,则该几何体的体积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | b>a>c | B. | c>b>a | C. | b>c>a | D. | a>b>c |