题目内容
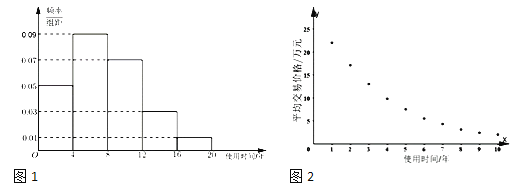
【题目】近年来,随着我国汽车消费水平的提高,二手车流通行业得到迅猛发展.某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.
附注:①对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为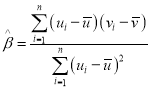 ,
,![]() ;
;
②参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)记“在2017年成交的二手车中随机选取一辆,该车的使用年限在![]() ”为事件
”为事件![]() ,试估计
,试估计![]() 的概率;
的概率;
(Ⅱ)根据该汽车交易市场的历史资料,得到散点图如图2,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用
(单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用![]() 作为二手车平均交易价格
作为二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ,
,![]() ):
):
|
|
|
|
|
|
5.5 | 8.7 | 1.9 | 301.4 | 79.75 | 385 |
①根据回归方程类型及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格![]() 的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格![]() 的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
【答案】(1)![]() (2)①
(2)①![]() ,②
,②![]() 万元
万元
【解析】
(1)由频率分布直方图求得该汽车交易市场2017年成交的二手车使用时间在![]() 与
与![]() 的频率,作和估计
的频率,作和估计![]() 的概率;
的概率;
(2)①由![]() 得,
得,![]() ,即
,即![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .分别求得
.分别求得![]() 与
与![]() 的值,则
的值,则![]() 关于
关于![]() 的线性回归方程可求,进一步得到
的线性回归方程可求,进一步得到![]() 关于
关于![]() 的回归方程;
的回归方程;
②根据①中求出的回归方程和图1,对成交的二手车在不同区间逐一预测,即可求得该汽车交易市场对于成交的每辆车可获得的平均佣金.
解:(1)由题得,二手车使用时间在![]() 的频率为
的频率为![]() ,
,
在![]() 的频率为
的频率为![]() ,
,
∴![]() ;
;
(2)①由题得,![]() ,即
,即![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
∵
![]() ,
,
![]() ,
,
∴![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,即
,即![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ;
;
②根据①中的回归方程![]() 和图1,对成交的二手车可预测:
和图1,对成交的二手车可预测:
使用时间在![]() 的平均成交价格为
的平均成交价格为![]() ,对应的频率为0.2;
,对应的频率为0.2;
使用时间在![]() 的平均成交价格为
的平均成交价格为![]() ,对应的频率为0.36;
,对应的频率为0.36;
使用时间在![]() 的平均成交价格为
的平均成交价格为![]() ,对应的频率为0.28;
,对应的频率为0.28;
使用时间在![]() 平均成交价格为
平均成交价格为![]() ,对应的频率为0.12;
,对应的频率为0.12;
使用时间在![]() 的平均成交价格为
的平均成交价格为![]() ,对应的频率为0.04.
,对应的频率为0.04.
∴该汽车交易市场对于成交的每辆车可获得的平均佣金为![]()
![]() 万元.
万元.

【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
附: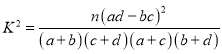
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
则下列说法正确的是( )
A.有![]() 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”
B.有![]() 以上的把握认为“爱好该项运动与性别无关”
以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过![]() 的前提下,认为“爱好该项运动与性别有关”
的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过![]() 的前提下,认为“爱好该项运动与性别有关”
的前提下,认为“爱好该项运动与性别有关”
【题目】某工厂每年定期对职工进行培训以提高工人的生产能力(生产能力是指一天加工的零件数).现有![]() 、
、![]() 两类培训,为了比较哪类培训更有利于提高工人的生产能力,工厂决定从同一车间随机抽取100名工人平均分成两个小组分别参加这两类培训.培训后测试各组工人的生产能力得到如下频率分布直方图.
两类培训,为了比较哪类培训更有利于提高工人的生产能力,工厂决定从同一车间随机抽取100名工人平均分成两个小组分别参加这两类培训.培训后测试各组工人的生产能力得到如下频率分布直方图.
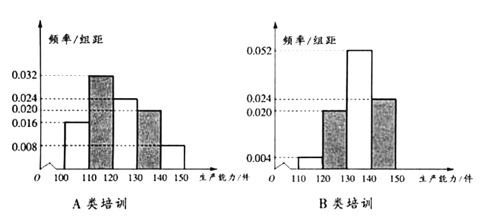
(1)记![]() 表示事件“参加
表示事件“参加![]() 类培训工人的生产能力不低于130件”,估计事件
类培训工人的生产能力不低于130件”,估计事件![]() 的概率;
的概率;
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为工人的生产能力与培训类有关:
的把握认为工人的生产能力与培训类有关:
生产能力 | 生产能力 | 总计 | |
| 50 | ||
| 50 | ||
总计 | 100 |
(3)根据频率分布直方图,判断哪类培训更有利于提高工人的生产能力,请说明理由.
参考数据
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.