题目内容
定义在定义域D内的函数y=f(x),若对任意的x1、x2∈D,都有|f(x1)-f(x2)|<1,则称函数y=f(x)为“Storm函数”.已知函数f(x)=x3-x+a(x∈[-1,1],a∈R).
(1)若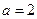 ,求过点
,求过点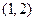 处的切线方程;
处的切线方程;
(2)函数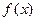 是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由.
是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由.
(1)若
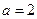 ,求过点
,求过点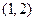 处的切线方程;
处的切线方程;(2)函数
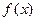 是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由.
是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由.(1)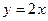 (2)当c≤-
(2)当c≤-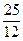 时,ax2+bx+c≤0的解集为R
时,ax2+bx+c≤0的解集为R
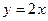 (2)当c≤-
(2)当c≤-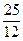 时,ax2+bx+c≤0的解集为R
时,ax2+bx+c≤0的解集为R 本题属于信息迁移题,主要考查利用导数求函数的极值.(1) ,
,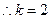 ,
,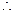 切线方程为
切线方程为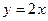 .
.
(2)函数f(x)=x3-x+a(x∈[-1,1],a∈R)的导数是f′(x)=3x2-1,
当3x2-1=0时,即x=±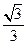 ,
,
当x<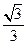 时,f′(x)=3x2-1<0;当x>
时,f′(x)=3x2-1<0;当x>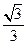 时,f′(x)=3x2-1>0,
时,f′(x)=3x2-1>0,
故f(x)在x∈[-1,1]内的极小值是a-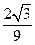 .
.
同理,f(x)在x∈[-1,1]内的极大值是a+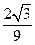 .
.
∵f(1)=f(-1)=a,
∴函数f(x)=x3-x+a(x∈[-1,1],a∈R)的最大值是a+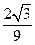 ,最小值是a-
,最小值是a-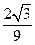 ,
,
因为|f(x1)-f(x2)|<|fmax-fmin|,
故|f(x1)-f(x2)|<|fmax-fmin|=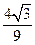 <1.
<1.
所以函数f(x)=x3-x+a(x∈[-1,1],a∈R)是“Storm函数”.
 ,
,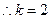 ,
,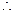 切线方程为
切线方程为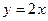 .
.(2)函数f(x)=x3-x+a(x∈[-1,1],a∈R)的导数是f′(x)=3x2-1,
当3x2-1=0时,即x=±
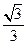 ,
,当x<
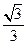 时,f′(x)=3x2-1<0;当x>
时,f′(x)=3x2-1<0;当x>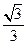 时,f′(x)=3x2-1>0,
时,f′(x)=3x2-1>0,故f(x)在x∈[-1,1]内的极小值是a-
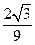 .
.同理,f(x)在x∈[-1,1]内的极大值是a+
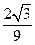 .
.∵f(1)=f(-1)=a,
∴函数f(x)=x3-x+a(x∈[-1,1],a∈R)的最大值是a+
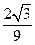 ,最小值是a-
,最小值是a-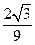 ,
,因为|f(x1)-f(x2)|<|fmax-fmin|,
故|f(x1)-f(x2)|<|fmax-fmin|=
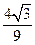 <1.
<1.所以函数f(x)=x3-x+a(x∈[-1,1],a∈R)是“Storm函数”.

练习册系列答案
相关题目
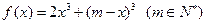 .
.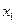 、
、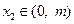 ,求证:①
,求证:①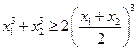 ;
;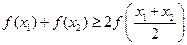 .
.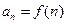 ,
,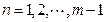 ,其中
,其中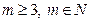 ,求证:
,求证: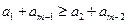 ;
;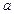 、
、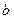 、
、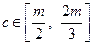 ,问:以
,问:以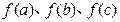 的值为长的三条线段是否可构成三角形?请说明理由.
的值为长的三条线段是否可构成三角形?请说明理由. 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .(Ⅰ)求
.(Ⅰ)求 的值;(Ⅱ)若方程
的值;(Ⅱ)若方程 在
在 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数);(Ⅲ)令
为自然对数的底数);(Ⅲ)令 ,若
,若 的图象与
的图象与 轴交于
轴交于 ,
, (其中
(其中 ),
), 的中点为
的中点为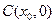 ,求证:
,求证: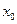 处的导数
处的导数 .
.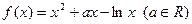 .
.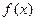 在
在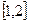 上是减函数,求实数
上是减函数,求实数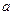 的取值范围;
的取值范围;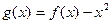 ,是否存在实数
,是否存在实数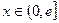 时,函数
时,函数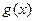 的最小值是
的最小值是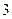 ,若存在,求出实数
,若存在,求出实数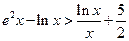 .
.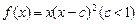 在区间
在区间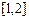 上的最小值为4,求
上的最小值为4,求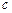 的值.
的值.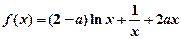 (a∈R).
(a∈R).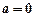 时,求
时,求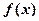 的极值;
的极值;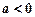 时,求
时,求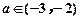 及
及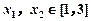 ,恒有
,恒有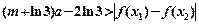
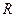 上的函数
上的函数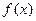 满足
满足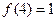 ,
,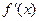 为
为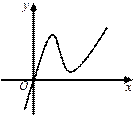
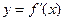 的图像如右图所示,
的图像如右图所示,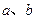 满足
满足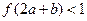 ,则
,则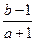 的取值范围是 .
的取值范围是 .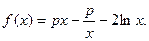
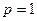 ,函数
,函数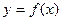 是否有极值,若有则求出极值,若没有,请说明理由.
是否有极值,若有则求出极值,若没有,请说明理由.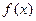 在其定义域内为单调函数,求实数p的取值范围.
在其定义域内为单调函数,求实数p的取值范围. ,
, ,函数
,函数 的图象与
的图象与 轴的交点也在函数
轴的交点也在函数 的图象上,且在此点有公共切线.
的图象上,且在此点有公共切线. 、
、 的值;
的值; 的大小.
的大小.