Question

【题目】已知函数，．

（Ⅰ）若在内单调递减，求实数的取值范围；

（Ⅱ）若函数有两个极值点分别为，，证明：．

Answer 1

【答案】（Ⅰ）（Ⅱ）见证明

【解析】

（I）先求得函数的导数，根据函数在上的单调性列不等式，分离常数后利用构造函数法求得的取值范围.（II）将极值点代入导函数列方程组，将所要证明的不等式转化为证明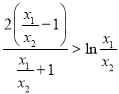，利用构造函数法证得上述不等式成立.

（I）．

∴在内单调递减，

∴在内恒成立，

即在内恒成立．

令，则，

∴当时，，即在内为增函数；

当时，，即在内为减函数．

∴的最大值为，

∴

（Ⅱ）若函数有两个极值点分别为，，

则在内有两根，，

由（I），知．

由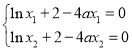，两式相减，得．

不妨设，

∴要证明，只需证明．

即证明，亦即证明．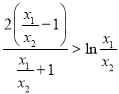

令函数．

∴，即函数在内单调递减．

∴时，有，∴．

即不等式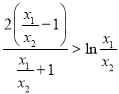成立．

综上，得．