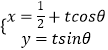题目内容
【题目】有一容量为50的样本,数据的分组以及各组的频数如下:
[12.5,15.5),3;[15.5,18.5),8;[18.5,21.5),9;[21.5,24.5),11;[24.5,27.5),10;[27.5,30.5),5;[30.5,33.5],4.
(1)列出样本的频率分布表.
(2)画出频率分布直方图.
(3)根据频率分布表,估计数据落在[15.5,24.5)内的可能性约是多少?
【答案】(1) 见解析.(2) 见解析.(3)0.56.
【解析】试题分析:(1)由题中的所给数据,列成表格,即可得到频率分布表中的数据;
(2)由频率分布表中的数据,在横轴为数据,纵轴为![]() ,即可得到频率分布直方图;
,即可得到频率分布直方图;
(3)为了估计数据在[15.5,24.5)的概率,只须求出频率分布直方图中数据在[15.5,24.5)的频率和即可.
试题解析:(1)频率分布表为:
分组 | 频数 | 频率 |
[12.5,15.5) | 3 | 0.06 |
[15.5,18.5) | 8 | 0.16 |
[18.5,21.5) | 9 | 0.18 |
[21.5,24.5) | 11 | 0.22 |
[24.5,27.5) | 10 | 0.20 |
[27.5,30.5) | 5 | 0.10 |
[30.5,33.5] | 4 | 0.08 |
合计 | 50 | 1.00 |
(2)频率分布直方图如图所示:

(3)数据落在[15.5,24.5)内的可能性为![]() =0.56.
=0.56.
点晴:本题考查的是用样本估计总体的分布.解决总体分布估计问题的一般程序如下: (1)先确定分组的组数(获得最大数据与最小数据,再根据最大数据与最小数据之差除组距得组数); (2)分别计算各组的频数及频率(频率![]() );(3)画出频率分布直方图,并作出相应的估计.
);(3)画出频率分布直方图,并作出相应的估计.

【题目】2014年山东省第二十三届运动会将在济宁召开,为调查我市某校高中生是否愿意提供志愿者服务,用简单随机抽样方法从该校调查了50人,结果如下:K
是否愿意提供志愿者服务 | 愿意 | 不愿意 |
男生 | 20 | 5 |
女生 | 10 | 15 |
(Ⅰ)用分层抽样的方法在愿意提供志愿者服务的学生中抽取6人,其中男生抽取多少人?
(Ⅱ)在(Ⅰ)中抽取的6人中任选2人,求恰有一名女生的概率;
(Ⅲ)你能否有99%的把握认为该校高中生是否愿意提供志愿者服务与性别有关?
下面的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
独立性检验统计量 ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
【题目】炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,因此必须掌握钢水含碳量和冶炼时间的关系.如果已测得炉料熔化完毕时,钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出钢的时间)的一些数据,如下表所示:
x/0.01% | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
y/min | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
(1)作出散点图,你能从散点图中发现含碳量与冶炼时间的一般规律吗?
(2)求回归直线方程.
(3)预测当钢水含碳量为160时,应冶炼多少分钟?