题目内容
【题目】某连锁分店销售某种商品,该商品每件的进价为![]() 元,预计当每件商品售价为
元,预计当每件商品售价为![]() 元时,一年的销售量(单位:万件)
元时,一年的销售量(单位:万件) 该分店全年需向总店缴纳宣传费、保管费共计
该分店全年需向总店缴纳宣传费、保管费共计![]() 万元.
万元.
(1)求该连锁分店一年的利润与每件商品售价![]() 的函数关系式
的函数关系式![]() ;
;
(2)求当每件商品售价为多少元时,该连锁店一年的利润最大,并求其最大值.
【答案】(1)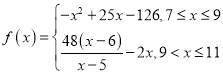 (2)每件商品售价为
(2)每件商品售价为![]() 元时,该连锁店一年利润最大,最大利润为
元时,该连锁店一年利润最大,最大利润为![]() 万元.
万元.
【解析】
(1)由利润与售价的关系,分段列出函数关系即可;
(2)分段分别利用二次函数性质,均值不等式求解最大值,即得解.
(1)①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ,
,
所以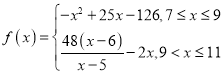 .
.
(2)①当![]() 时,
时,![]() ,
,
其对称轴为![]() ,所当
,所当![]() 时,
时,![]() 有最大值
有最大值![]() .
.
②当![]() 时,
时,![]() ,设
,设![]() ,
,
![]() ,
,
当且仅当![]() ,即
,即![]() 取等号.因为
取等号.因为![]() .
.
答:每件商品售价为![]() 元时,该连锁店一年利润最大,最大利润为
元时,该连锁店一年利润最大,最大利润为![]() 万元.
万元.

练习册系列答案
相关题目
【题目】某班主任对全班50名学生学习积极性和对待工作的态度进行了调查,统计数据如下所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法有多大把握认为学生的学习积极性与对班级工作的态度有关系?并说明理由.
本题参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |


